
如图,O是半径为1的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,
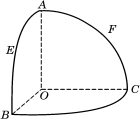
⑴求点E、F在该球面上的球面距离;
⑵求平面OEF与平面OBC所成的锐二面角.(用反三角函数表示)
|
解:⑴解法一:如图,证明0M=0N=MN= ∴点E、F在该球面上的球面距离为
解法二:如图,补形易证:∠EOF=∠GOH=
解法三:其实 解法四:如图,建立空间直角坐标系,易知E( ∴
⑵解法一:如图,取BC中点P,连接AP交MN与Q,则易证,∠POQ就是所求二面角的平面角. 在三角形OPQ中,OP= ∴∠POQ=arcos
解法二:如图,补形成正方体去解决.
解法三:如图,建立空间直角坐标系去求解.
|


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
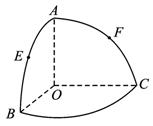
如图,O是半径为1的球心,点A、B、C在球面上,
OA、OB、OC两两垂直,E、F分别为大圆弧AB与
AC的中点,则点E、F在该球上的球面距离是??????______
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省邯郸市高三第二次模拟考试文科数学卷 题型:选择题
如图,O是半径为1的球的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别为大圆弧AB与AC的中点,则E、F的球面距离是_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com