
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,点
,点![]() 是坐标平面内一点,且
是坐标平面内一点,且![]() ,
, ![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的动直线
的动直线![]() 交椭圆于
交椭圆于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使以
,使以![]() 为直径的圆恒过该点?若存在,求出点
为直径的圆恒过该点?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() .
.
【解析】试题分析:(1)设![]() 的坐标,利用
的坐标,利用![]() 和
和![]() 求得c,通过椭圆的离心率求得a,最后利用a,b和c的关系求出b,则椭圆的方程可得.
求得c,通过椭圆的离心率求得a,最后利用a,b和c的关系求出b,则椭圆的方程可得.
(2)设出直线l的方程,与椭圆方程联立消去y,设![]() ,
, ![]() ,则可根据韦达定理表示出
,则可根据韦达定理表示出![]() 和
和![]() ,假设在y轴上存在定点
,假设在y轴上存在定点![]() ,满足题设,则可表示出
,满足题设,则可表示出![]() ,利用
,利用![]() ,求出m的值
,求出m的值
试题解析:(1)设![]() ,
, ![]() ,
, ![]() ,则由
,则由![]() ,得
,得![]() ;
;
由![]() 得
得![]() ,
,
即![]() .
.
所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
因此所求椭圆的方程为: ![]() .
.
(2)设动直线![]() 的方程为:
的方程为: ![]() ,
,
由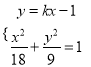 得
得![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
假设在![]() 轴上是否存在定点
轴上是否存在定点![]() ,满足题设,则
,满足题设,则![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
由假设得对于任意的![]() ,
, ![]() 恒成立,
恒成立,
即![]() 解得
解得![]() .
.
因此,在![]() 轴上存在定点
轴上存在定点![]() ,使以
,使以![]() 为直径的圆恒过该点,
为直径的圆恒过该点,
点![]() 的坐标为
的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】给出以下四个问题:①x,输出它的绝对值.②求面积为6的正方形的周长.③求三个数a,b,c中最大数.④求函数![]() 的函数值.其中不需要用条件语句来描述其算法的有 个.
的函数值.其中不需要用条件语句来描述其算法的有 个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列{an}的各项均为正数,其前n项和为Sn , 若a1=1,a3=4.
(1)若Sk=63,求k的值;
(2)设bn=log2an , 证明数列{bn}是等差数列;
(3)设cn=(﹣1)nbn , 求T=|c1|+|c2|+|c3|+…+|cn|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率;
(2)检验结束后,甲、乙两名运动员的成绩如下:
甲:70,68,74,71,72
乙:70,69,70,74,72
根据两组数据完成图示的茎叶图,并通过计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中A(3,﹣1),AB边上的中线CM所在直线方程为6x+10y﹣59=0,∠B的平分线方程BT为x﹣4y+10=0.
(1)求顶点B的坐标;
(2)求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是( ) 
A.i=2017?
B.i≥2017?
C.i≥2018?
D.i≤2018?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com