
分析 (Ⅰ)当$k=\frac{1}{2}$时,化简函数f(x)的解析式,利用函数的导数求解函数的单调区间和极值;
(Ⅱ)当0<k<1时,求出函数f(x)在区间[1,e]上的最大值,然后判断结果即可.
解答 解:(Ⅰ)因为$f(x)=kx-(k+1)lnx-\frac{1}{x}$,
所以$f'(x)=k-\frac{k+1}{x}+\frac{1}{x^2}=\frac{{k{x^2}-(k+1)x+1}}{x^2}$,….(1分)
当$k=\frac{1}{2}$时,$f'(x)=\frac{{\frac{1}{2}(x-2)(x-1)}}{x^2}$.….(2分)
令$f'(x)=\frac{{\frac{1}{2}(x-2)(x-1)}}{x^2}=0$,得x1=1,x2=2,….(3分)
所以f′(x),f(x)随x的变化情况如下表:
| x | (0,1) | 1 | (1,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
| x | $(1,\frac{1}{k})$ | $\frac{1}{k}$ | $(\frac{1}{k},e)$ |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,函数的最值的求法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{3}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
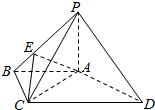 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | (-2,2) | C. | (-∞,-2]∪[2,+∞) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com