
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ;
;
②函数![]() 有2个零点;
有2个零点;
③![]() 的解集为
的解集为![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命题的个数为( )
A.4B.3C.2D.1
【答案】C
【解析】
对于①,利用函数![]() 是定义在R上的奇函数求解即可;对于②,由函数解析式及函数为奇函数求解即可;对于③,分别解当
是定义在R上的奇函数求解即可;对于②,由函数解析式及函数为奇函数求解即可;对于③,分别解当![]() 时,当
时,当![]() 时,
时,![]() 即可得解;对于④,利用导数研究函数的单调性,再求值域即可得解.
即可得解;对于④,利用导数研究函数的单调性,再求值域即可得解.
解:对于①,函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]()
![]() ,即①错误;
,即①错误;
对于②,由题意可得![]() ,即函数
,即函数![]() 有3个零点,即②错误;
有3个零点,即②错误;
对于③,当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]()
![]() ,令
,令![]() ,解得
,解得![]() ,综上可得
,综上可得![]() 的解集为
的解集为![]() ,即③正确;
,即③正确;
对于④,当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,即函数
,即函数![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,即函数在
为增函数,即函数在![]() 的最小值为
的最小值为![]() ,且
,且![]() 时,
时,![]() ,又
,又![]() ,则
,则![]() ,由函数为奇函数可得当
,由函数为奇函数可得当![]() 时,
时,![]() ,又
,又![]() ,即函数
,即函数![]() 的值域为
的值域为![]() ,即
,即![]() ,
,![]() ,都有
,都有![]() ,即④正确,
,即④正确,
即真命题的个数为2,
故选:C.


科目:高中数学 来源: 题型:
【题目】已知经过圆![]() 上点
上点![]() 的切线方程是
的切线方程是![]() .
.
(1)类比上述性质,直接写出经过椭圆![]() 上一点
上一点![]() 的切线方程;
的切线方程;
(2)已知椭圆![]() ,P为直线
,P为直线![]() 上的动点,过P作椭圆E的两条切线,切点分别为AB,
上的动点,过P作椭圆E的两条切线,切点分别为AB,
①求证:直线AB过定点.
②当点P到直线AB的距离为![]() 时,求三角形PAB的外接圆方程.
时,求三角形PAB的外接圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民收入也逐年增加.为了更好的制定2019年关于加快提升农民年收入力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收入并制成如下频率分布直方图:
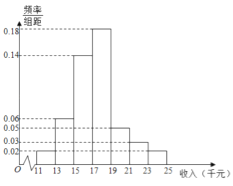
附:参考数据与公式 ![]() ,若
,若 ![]() ,则①
,则① ![]() ;②
;② ![]() ;③
;③ ![]() .
.
(1)根据频率分布直方图估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图可以认为该贫困地区农民年收入 X 服从正态分布 ![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() 近似为样本方差
近似为样本方差![]() ,经计算得:
,经计算得:![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每个农民的年收入相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在校园篮球赛中,甲、乙两个队10场比赛的得分数据整理成如图所示的茎叶图,下列说法正确的是( )
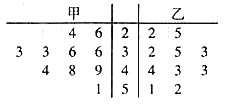
A.乙队得分的中位数是38.5
B.甲、乙两队得分在![]() 分数段频率相等
分数段频率相等
C.乙队的平均得分比甲队的高
D.甲队得分的稳定性比乙队好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题,大概意思如下:在下雨时,用一个圆台形的天池盆接雨水,天池盆盆口直径为2尺8寸,盆底直径为1尺2寸,盆深1尺8寸.若盆中积水深9寸,则平均降雨量是(注:①平均降雨量等于盆中积水体积除以盆口面积;②1尺等于10寸;③台体的体积![]()
![]() )( )
)( )
A.3寸B.4寸C.5寸D.6寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假期间,某高中决定深入调查本校学生寒假期间在家学习情况,并将依据调查结果对相应学生提出针对性学习建议.现从本校高一、高二、高三三个年级中分别随机选取30,45,75人,然后再从这些学生中抽取10人,进行学情调查.
(1)若采用分层抽样抽取10人,分别求高一、高二、高三应抽取的人数.
(2)若被抽取的10人中,有6人每天学时超过7小时,有4人每天学时不足4小时,现从这10人中,再随机抽取4人做进一步调查.
(i)记事件A为“被抽取的4人中至多有1人学时不足4小时”,求事件A发生的概率;
(ii)用ξ表示被抽取的4人中学时不足4小时的人数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 为参数
为参数![]() ,圆C的标准方程为
,圆C的标准方程为![]() 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
![]() 求直线l和圆C的极坐标方程;
求直线l和圆C的极坐标方程;
![]() 若射线
若射线![]() 与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB的中点,求a的值.
与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB的中点,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com