
【题目】如图,已知抛物线E:![]() (
(![]() )与圆O:
)与圆O:![]() 相交于A,B两点,且
相交于A,B两点,且![]() .过劣弧
.过劣弧![]() 上的动点
上的动点![]() 作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线
作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线![]() ,
,![]() ,相交于点M.
,相交于点M.
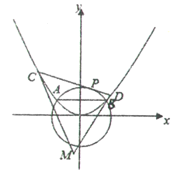
(1)求抛物线E的方程;
(2)求点M到直线![]() 距离的最大值.
距离的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用![]() 求得圆心
求得圆心![]() 到弦
到弦![]() 的距离为1,即可求得点
的距离为1,即可求得点![]() 的坐标为
的坐标为![]() ,将
,将![]() 代入抛物线方程可得
代入抛物线方程可得![]() ,问题得解
,问题得解
(2)设![]() ,
,![]() ,分别求得
,分别求得![]() 与
与![]() 的方程,即可求得点
的方程,即可求得点![]() 的横、纵坐标为
的横、纵坐标为![]() ,
,![]() ,联立直线
,联立直线![]() 的方程和抛物线方程可得:
的方程和抛物线方程可得:![]() ,
,![]() ,即可得点
,即可得点![]() 的横、纵坐标为
的横、纵坐标为![]() ,
,![]() ,再由点到直线距离公式可得点M到直线
,再由点到直线距离公式可得点M到直线![]() 的距离为:
的距离为: ,
,![]() ,利用其单调性可得:
,利用其单调性可得:![]() ,问题得解
,问题得解
(1)![]()
![]() ,且B在圆上,
,且B在圆上,
所以圆心![]() 到弦
到弦![]() 的距离
的距离![]()
由抛物线和圆的对称性可得![]() ,
,
代入抛物线可得![]() ,解得
,解得![]() ,
,
∴抛物线E的方程为![]() ;
;
(2)设![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
则![]() 的方程为:
的方程为:![]() ,即
,即![]() ——①,
——①,
同理![]() 的方程为:
的方程为:![]() ——②,
——②,
联立①②解得![]() ,
,![]() ,
,
又直线![]() 与圆
与圆![]() 切于点
切于点![]() ,
,
易得![]() 方程为
方程为![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,
联立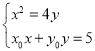 ,化简得
,化简得![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴点M到直线![]() 的距离为:
的距离为:
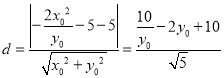 ,
,![]()
易知d关于![]() 单调递减,
单调递减,![]() ,
,
即点M到直线![]() 距离的最大值为
距离的最大值为![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为A,右焦点为F,O是坐标原点,
的上顶点为A,右焦点为F,O是坐标原点,![]() 是等腰直角三角形,且周长为
是等腰直角三角形,且周长为![]() .
.
(1)求椭圆的方程;
(2)若直线l与AF垂直,且交椭圆于B,C两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆E的一个焦点与抛物线![]() 的焦点关于直线
的焦点关于直线![]() 对称,且椭圆E与坐标轴的一个交点坐标为
对称,且椭圆E与坐标轴的一个交点坐标为![]() .
.
(1)求椭圆E的标准方程;
(2)过点![]() 的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究
的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情后,为了支持企业复工复产,某地政府决定向当地企业发放补助款,其中对纳税额在![]() 万元至
万元至![]() 万元(包括
万元(包括![]() 万元和
万元和![]() 万元)的小微企业做统一方案.方案要求同时具备下列两个条件:①补助款
万元)的小微企业做统一方案.方案要求同时具备下列两个条件:①补助款![]() (万元)随企业原纳税额
(万元)随企业原纳税额![]() (万元)的增加而增加;②补助款不低于原纳税额
(万元)的增加而增加;②补助款不低于原纳税额![]() (万元)的
(万元)的![]() .经测算政府决定采用函数模型
.经测算政府决定采用函数模型![]() (其中
(其中![]() 为参数)作为补助款发放方案.
为参数)作为补助款发放方案.
(1)判断使用参数![]() 是否满足条件,并说明理由;
是否满足条件,并说明理由;
(2)求同时满足条件①、②的参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
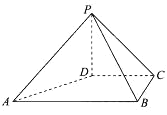
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系![]() 中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为:
中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为:![]() ,倾斜角为锐角的直线l过点
,倾斜角为锐角的直线l过点![]() 与单位圆
与单位圆![]() 相切.
相切.
(1)求曲线C的直角坐标方程和直线l的参数方程;
(2)设直线l与曲线C交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
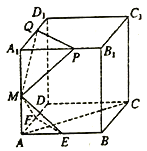
【题目】如图,已知在棱长为1的正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,又
的中点,又![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上,且
上,且![]() .设平面
.设平面![]() 平面
平面![]() ,现有下列结论:
,现有下列结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③直线![]() 与平面
与平面![]() 不垂直;
不垂直;
④当![]() 变化时,
变化时,![]() 不是定直线.
不是定直线.
其中不成立的结论是______.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com