
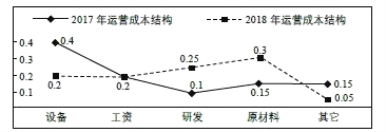
����Ŀ��ij��ҵ�����ִ����������ƣ�����Ч���������.2018��ȫ����������2017��ȫ�����������������һ����ʵ�ַ���.ͬʱ����ҵ�ĸ�����Ӫ�ɱ�Ҳ��������ı仯��������Ӧ�仯.��ͼ�����˸���ҵ�����겻ͬ��Ӫ�ɱ�ռȫ��������ı���������˵����ȷ���ǣ� ��
A.����ҵ2018��ԭ���Ϸ�����2017�깤�ʽ�����з����õĺ�
B.����ҵ2018���з�������2017�깤�ʽ�ԭ���Ϸ��á�������������ĺ�
C.����ҵ2018������������2017�깤�ʽ���![]()
D.����ҵ2018���豸������2017��ԭ���ϵķ��õ�����
���𰸡�B
��������
�ȶ�����ͼ��Ϣ�����⼰�������ٽ�����ݽ��мĺ���������һ���鼴�ɵý⣮
�⣺������ͼ��֪��������2017��ȫ�������Ϊt����2018��ȫ�������Ϊ2t.
����ѡ��A������ҵ2018��ԭ���Ϸ���Ϊ0.3��2t��0.6t��2017�깤�ʽ�����з����õĺ�Ϊ0.2t+0.1t��0.3t����A����
����ѡ��B������ҵ2018���з�����Ϊ0.25��2t��0.5t��2017�깤�ʽ�ԭ���Ϸ��á�������������ĺ�Ϊ0.2t+0.15t+0.15t��0.5t����B��ȷ��
����ѡ��C������ҵ2018������������0.05��2t��0.1t��2017�깤�ʽ����0.2t����C����
����ѡ��D������ҵ2018���豸������0.2��2t��0.4t��2017��ԭ���ϵķ�����0.15t����D����.
��ѡ��![]() .
.


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��x2��2py��p��0���Ľ���ΪF��ֱ��l��������C����P��Q���㣮
��1����l����F��������C�ڵ�P�����������ڵ�Q�������߽��ڵ�G��֤������G�ڶ�ֱ���ϣ�
��2����p��2����M������y![]() �ϣ�MP��MQ���е����������C�ϣ����MPQ�����ȡֵ��Χ��
�ϣ�MP��MQ���е����������C�ϣ����MPQ�����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �У�
�У�![]() ��D��E��F�ֱ�Ϊ�߶�
��D��E��F�ֱ�Ϊ�߶�![]() ��
��![]() ��
��![]() ���е�.
���е�.
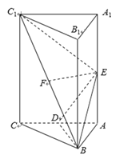
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2��֤����![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�綯��������ҵ������������綯����Ͷ��ɱ�Ϊ1��Ԫ/����������Ϊ1.2��Ԫ/������������Ϊ1000���������Ϊ��Ӧ�г����ƻ���߲�Ʒ���Σ��ʶ�����Ͷ��ɱ�����ÿ����Ͷ��ɱ����ӵı���Ϊ![]() �����������Ӧ��ߵı���Ϊ
�����������Ӧ��ߵı���Ϊ![]() ���ҵ�
���ҵ�![]() ������0.5ʱ��Ԥ�������������ӵı���Ϊ
������0.5ʱ��Ԥ�������������ӵı���Ϊ![]() ������
������![]() ����0.5ʱ��Ԥ�������������䣮��֪������=�������ۣ�Ͷ��ɱ��������������������Ԥ�Ƶ�������
����0.5ʱ��Ԥ�������������䣮��֪������=�������ۣ�Ͷ��ɱ��������������������Ԥ�Ƶ�������![]() ��Ͷ��ɱ����ӵı���
��Ͷ��ɱ����ӵı���![]() �Ĺ�ϵʽΪ______��Ϊʹ���������������������ӣ�Ͷ��ɱ����ӵı���
�Ĺ�ϵʽΪ______��Ϊʹ���������������������ӣ�Ͷ��ɱ����ӵı���![]() ��ȡֵ��ΧΪ______��
��ȡֵ��ΧΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]()
![]() ��eΪ��Ȼ�����ĵ�����
��eΪ��Ȼ�����ĵ�����
��1����f��x���ĵ������䣺
��2����ax2+x+a��exx+exlnx��0����������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��M����![]() �������N��
�������N��![]() ���У����M��Բ��M�Ĺ켣Ϊ����C��
���У����M��Բ��M�Ĺ켣Ϊ����C��
��1��������C�ķ��̣�
��2����ֱ��l��������![]() ��������C�ཻ��P��Q���㣮��ֱ��PB��ֱ��QB��б��֮��Ϊ
��������C�ཻ��P��Q���㣮��ֱ��PB��ֱ��QB��б��֮��Ϊ![]() ���ж�ֱ��l�Ƿ�����㣬�������㣬����˶������ꣻ���������㣬��˵�����ɣ�
���ж�ֱ��l�Ƿ�����㣬�������㣬����˶������ꣻ���������㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������
��������![]() ��
��![]() �ϴ���������ֵ��
�ϴ���������ֵ��![]() .
.
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ף������˽�����Ӳ����Ϸ���涨��ÿ���ױҺ��������ϼ�Ӯ��������Ӯ.��ʱ������������Ϸ����֪����Ӯ![]() (����
(����![]() )�ξͻ�ʤ������Ҫ��Ӯ
)�ξͻ�ʤ������Ҫ��Ӯ![]() (����
(����![]() )�βŻ�ʤ������һ�˻�ʤ��Ϸ�ͽ���.���ٽ���
)�βŻ�ʤ������һ�˻�ʤ��Ϸ�ͽ���.���ٽ���![]() ���ױң���Ϸ����.
���ױң���Ϸ����.
��1����![]() ��
��![]() �������
�������![]() ��
��
��2����![]() �������
�������![]() �����ֵ(��
�����ֵ(��![]() ��ʾ).
��ʾ).
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com