练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数满足:对于任意正数，都有，且，则称函数为“L函数”．

    （1）试判断函数与是否是“L函数”；

    （2）若函数为“L函数”，求实数a的取值范围；

    （3）若函数为“L函数”，且，求证：对任意，都有．

    【答案】（1）是“L函数”. 不是“L函数”.（2）（3）见解析

    【解析】（1）对于函数，当时，，

    又，所以，

    故是“L函数”.

    对于函数，当时，，

    故不是“L函数”.

    （2）当时，由是“L函数”，

    可知，即对一切正数恒成立，

    又，可得对一切正数恒成立，所以．

    由，可得，

    故，又，故

    由对一切正数恒成立，可得，即．

    综上可知，a的取值范围是．

    （3）由函数为“L函数”， 可知对于任意正数，

    都有，且，

    令，可知，即，

    故对于正整数k与正数，都有

    ，

    对任意，可得，又，

    所以，

    同理，

    故 ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”．兴趣小组同学实施如下方案来测量塔的倾斜度和塔高：如图，记O点为塔基、P点为塔尖、点P在地面上的射影为点H．在塔身OP射影所在直线上选点A，使仰角∠HAP=45°，过O点与OA成120°的地面上选B点，使仰角∠HPB=45°（点A、B、O都在同一水平面上），此时测得∠OAB=27°，A与B之间距离为33.6米．试求：

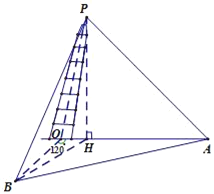
    （1）塔高（即线段PH的长，精确到0.1米）；

    （2）塔身的倾斜度（即PO与PH的夹角，精确到0.1°）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地政府为改善居民的住房条件，集中建设一批经适楼房．用了1400万元购买了一块空地，规划建设8幢楼，要求每幢楼的面积和层数等都一致，已知该经适房每幢楼每层建筑面积均为250平方米，第一层建筑费用是每平方米3000元，从第二层开始，每一层的建筑费用比其下面一层每平方米增加80元．

    （1）若该经适楼房每幢楼共层，总开发费用为万元，求函数的表达式（总开发费用=总建筑费用+购地费用）；

    （2）要使该批经适房的每平方米的平均开发费用最低，每幢楼应建多少层？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】曲线上动点到定点与定直线的距离之比为常数；

    （1）求曲线的轨迹方程；

    （2）设圆心为的圆与曲线交于点与点，求的最小值，并求此时圆的方程；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，下列个结论正确的是__________（把你认为正确的答案全部写上）．

    （1）任取，都有；

    （2）函数在上单调递增；

    （3），对一切恒成立；

    （4）函数有个零点；

    （5）若关于的方程有且只有两个不同的实根，，则.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥S-ABCD中，四边形ABCD是菱形，，，点P，Q，M分别是线段SD，PD，AP的中点，点N是线段SB上靠近B的四等分点．

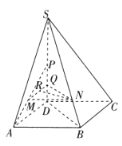
    （1）若R在直线MQ上，求证：平面ABCD；

    （2）若平面ABCD，求平面SAD与平面SBC所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（，为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线经过点，曲线的直角坐标方程为.

    （1）求曲线的普通方程，曲线的极坐标方程；

    （2）若，是曲线上两点，当时，求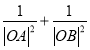的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，平面平面，和均是等腰直角三角形，，，、分别为、的中点.

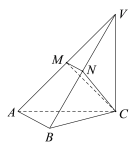
    （Ⅰ）求证：平面；

    （Ⅱ）求证：；

    （Ⅲ）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，如果存在给定的实数对，使得恒成立，则称为“函数”；

    （1）判断函数，是否是“函数”；

    （2）若是一个“函数”，求出所有满足条件的有序实数对；

    （3）若定义域为的函数是“函数”，且存在满足条件的有序实数对和，当时，的值域为，求当时的值域；

    查看答案和解析>>

    同步练习册答案