
【题目】下列命题中错误的是( )
A. 若两个平面平行,则分别位于这两个平面的直线也互相平行
B. 平行于同一个平面的两个平面平行;
C. 平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行
D. 若两个平面平行,则其中一个平面内的直线平行于另一个平面
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线![]() 的焦点,它的离心率是双曲线
的焦点,它的离心率是双曲线![]() 的离心率的倒数.
的离心率的倒数.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知真命题:“函数y=f(x)的图象关于点P(a,b)成中心对称图形”的充要条件为“函数y=f(x+a)﹣b 是奇函数”.
(1)将函数g(x)=x3﹣3x2的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数g(x)图象对称中心的坐标;
(2)求函数h(x)= ![]() 图象对称中心的坐标;
图象对称中心的坐标;
(3)已知命题:“函数 y=f(x)的图象关于某直线成轴对称图象”的充要条件为“存在实数a和b,使得函数y=f(x+a)﹣b 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径、圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.
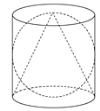
(1)试计算出图案中球与圆柱的体积比;
(2)假设球半径![]() .试计算出图案中圆锥的体积和表面积.
.试计算出图案中圆锥的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , x∈R.
(1)若直线y=kx+1与f (x)的反函数g(x)=lnx的图象相切,求实数k的值;
(2)设x>0,讨论曲线y=f (x) 与曲线y=mx2(m>0)公共点的个数.
(3)设a<b,比较 ![]() 与
与 ![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的60名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | 合计 | |
男生 | 20 | 10 | 30 |
女生 | 10 | 20 | 30 |
合计 | 30 | 30 | 60 |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选3人,求恰有2个男生和1个女生的概率.
下面的临界值表供参考:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=
的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF= ![]() ,则C的离心率e= .
,则C的离心率e= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com