
【题目】下列各对直线不互相垂直的是 ( )
A. l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B. l1的斜率为-![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q![]()
C. l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2![]() )
)
D. l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
科目:高中数学 来源: 题型:
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m、高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为a,M为BD1的中点,N在A1C1上,且满足|A1N|=3|NC1|.
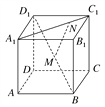
(1)求MN的长;
(2)试判断△MNC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
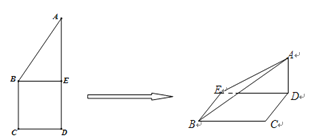
【题目】如图正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ∥
∥![]() ;
;
③![]() 的体积是
的体积是![]() ;
;
④平面![]() ⊥平面
⊥平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中正确的有 .(填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=90°,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG.
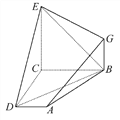
(1)求证:EC⊥CD.
(2)求证:AG∥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A(n)表示正整数n的个位数,an=A(n2)﹣A(n),A为数列{an}的前202项和,函数f(x)=ex﹣e+1,若函数g(x)满足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
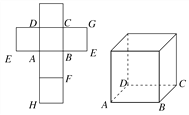
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】AB是☉O的直径,点C是☉O上的动点(点C不与A,B重合),过动点C的直线VC垂直于☉O所在的平面,D,E分别是VA,VC的中点,则下列结论中正确的是________(填写正确结论的序号).
(1)直线DE∥平面ABC.
(2)直线DE⊥平面VBC.
(3)DE⊥VB.
(4)DE⊥AB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(-![]() ,0),B(0,-
,0),B(0,-![]() ),其中k≠0且k≠±1,直线l经过点P(1,0)和AB的中点.
),其中k≠0且k≠±1,直线l经过点P(1,0)和AB的中点.
(1)求证:A,B关于直线l对称.
(2)当1<k<![]() 时,求直线l在y轴上的截距b的取值范围.
时,求直线l在y轴上的截距b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com