
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③![]() ;④当
;④当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,正确的个数为( )
,正确的个数为( )
A.1个B.2个C.3个D.以上都不对
【答案】B
【解析】
根据点M(a,b)与点![]() 在直线3x﹣4y+5=0的两侧,可以画出点M(a,b)所在的平面区域,进而结合二元一次不等式,两点之间距离公式的几何意义,及两点之间连线斜率的几何意义,逐一分析四个命题得结论.
在直线3x﹣4y+5=0的两侧,可以画出点M(a,b)所在的平面区域,进而结合二元一次不等式,两点之间距离公式的几何意义,及两点之间连线斜率的几何意义,逐一分析四个命题得结论.
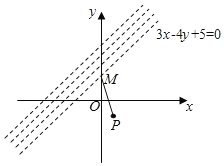
∵点M(a,b)与点![]() 在直线3x﹣4y+5=0的两侧,如图所示:点M(a,b)在直线3x﹣4y+5=0左上方的区域.
在直线3x﹣4y+5=0的两侧,如图所示:点M(a,b)在直线3x﹣4y+5=0左上方的区域.
∴(3a﹣4b+5)(3×1+4+5)<0,即3a﹣4b+5<0,故①错误;
当a>0时,由图可知,M的区域,不含边界,∴a+b即无最小值,也无最大值,故②错误;
设原点到直线3x﹣4y+5=0的距离为d,则d=![]() ,则a2+b2>1,故③正确;
,则a2+b2>1,故③正确;
当a>0且a≠1时,![]() 表示点M(a,b)与P(1,﹣1)连线的斜率,由图可知,
表示点M(a,b)与P(1,﹣1)连线的斜率,由图可知,
当a=0,b=![]() 时,
时,![]() =
=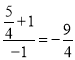 ,又直线3x﹣4y+5=0的斜率为
,又直线3x﹣4y+5=0的斜率为![]() ,
,
故![]() 的取值范围为(﹣∞,﹣
的取值范围为(﹣∞,﹣![]() )∪(
)∪(![]() ,+∞),故④正确.
,+∞),故④正确.
∴正确命题的个数是2个.
故选:B.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当a=1时,求函数![]() 在(2,
在(2,![]() )处的切线方程:
)处的切线方程:
(2)当a=2时,求函数![]() 的单调区间和极值;
的单调区间和极值;
(3)若![]() 在
在![]() 上是单调增函数,求实数a的取值范围.
上是单调增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取100件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
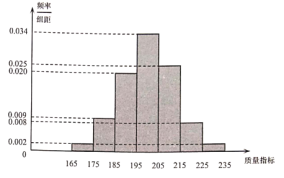
产品质量/毫克 | 频数 |
| 3 |
| 9 |
| 19 |
| 35 |
| 22 |
| 7 |
| 5 |
(1)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
(2)按照以往经验,在每小时次品数超过180件时,产品的次品率会大幅度增加,为检测公司的生产能力,同时尽可能控制不合格品总量,公司工程师抽取几组一小时生产产品数据进行次品情况检查分析,在![]() (单位:百件)件产品中,得到次品数量
(单位:百件)件产品中,得到次品数量![]() (单位:件)的情况汇总如下表所示:
(单位:件)的情况汇总如下表所示:
| 0.5 | 2 | 3.5 | 4 | 5 |
| 2 | 14 | 24 | 35 | 40 |
根据公司规定,在一小时内不允许次品数超过180件,请通过计算分析,按照公司的现有生产技术设备情况,判断可否安排一小时生产2000件的任务?
(参考公式:用最小二乘法求线性回方程![]() 的系数公式
的系数公式
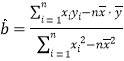
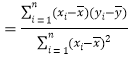 ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地的出租车价格规定:起步费![]() 元,可行
元,可行![]() 公里,
公里,![]() 公里以后按每公里
公里以后按每公里![]() 元计算,可再行
元计算,可再行![]() 公里;超过
公里;超过![]() 公里按每公里
公里按每公里![]() 元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定。
元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定。
(1)若小明乘出租车从学校到家,共![]() 公里,请问他应付出租车费多少元?
公里,请问他应付出租车费多少元?
(2)求车费![]() (元)与行车里程
(元)与行车里程![]() (公里)之间的函数关系式
(公里)之间的函数关系式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面为矩形的四棱锥![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
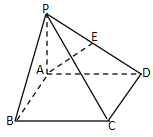
(1)求四棱锥![]() 的体积;
的体积;
(2)求![]() 与面
与面![]() 所成角;
所成角;
(3)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求出;若不存在,请说明理由.
?若存在,求出;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌![]() 与身高
与身高![]() 进行测量,得到数据(单位:cm)作为样本如表所示:
进行测量,得到数据(单位:cm)作为样本如表所示:
脚掌长( | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高( | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程![]() ;
;
(2)若某人的脚掌长为26.5cm,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人进行进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据: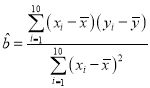 ,
, ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com