
【题目】已知函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)若![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上无解,求实数
上无解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由![]() ,结合不等式的基本性质可求出函数
,结合不等式的基本性质可求出函数![]() 的值域;
的值域;
(2)由![]() 求出
求出![]() ,再利用奇函数的定义证明函数
,再利用奇函数的定义证明函数![]() 为奇函数;
为奇函数;
(3)由(2)知函数![]() 为奇函数,且为增函数,由
为奇函数,且为增函数,由![]() 可得出
可得出![]() ,可得出方程
,可得出方程![]() 在
在![]() 上无解,构造函数
上无解,构造函数![]() ,分
,分![]() 、
、![]() 、
、![]() 三种情况讨论,结合二次函数的性质列出关于
三种情况讨论,结合二次函数的性质列出关于![]() 的不等式(组)求解.
的不等式(组)求解.
(1)![]() ,
,![]() ,则
,则![]() ,因此,函数
,因此,函数![]() 的值域为
的值域为![]() ;
;
(2)![]() 为奇函数,且定义域为
为奇函数,且定义域为![]() ,
,
则![]() ,解得
,解得![]() ,此时,
,此时,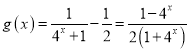 ,
,
则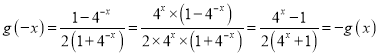 ,
,
所以,函数![]() 为奇函数;
为奇函数;
(3)由(2)知,函数![]() 为奇函数,
为奇函数,
由![]() ,可得
,可得![]() ,
,
即![]() ,
,
由于函数![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,即
,即![]() ,
,
由题意可知,方程![]() 在
在![]() 上无解.
上无解.
构造函数![]() ,该二次函数图象开口向上,对称轴为直线
,该二次函数图象开口向上,对称轴为直线![]() .
.
①当![]() 时,即当
时,即当![]() 时,则函数
时,则函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以,![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,此时
,此时![]() ;
;
②当![]() 时,即当
时,即当![]() 时,由于
时,由于![]() ,
,
则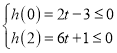 ,解得
,解得![]() ,此时
,此时![]() ;
;
③当![]() 时,即当
时,即当![]() 时,则函数
时,则函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,此时
,此时![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如图频率分布直方图:
五组,并作出如图频率分布直方图:
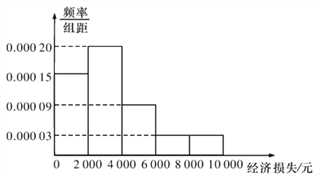
(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过4000元的居民中随机抽取2户进行捐款援助,设抽出损失超过8000元的居民为![]() 户,求
户,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如图,根据图表格中所给数据,分别求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并说明是否有
的值,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 |
|
| |
捐款不超过500元 |
|
| |
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且tan∠EAB=![]() .
.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE,证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
(2)能否在犯错误的概率不超过百分之一的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴上,抛物线C上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
![]() Ⅰ
Ⅰ![]() 求抛物线C的标准方程;
求抛物线C的标准方程;
![]() Ⅱ
Ⅱ![]() 设点
设点![]() ,过点
,过点![]() 的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为
的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为![]() ,
,![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到定点
到定点![]() 的距离之比它到直线
的距离之比它到直线![]() 的距离小1,设动点
的距离小1,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两个不同的点,过点
两个不同的点,过点![]() 分别作曲线
分别作曲线![]() 的切线,且二者相交于点
的切线,且二者相交于点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求证:![]() ;
;
(3)求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)求过点A(2,6)且在两坐标轴上的截距相等的直线m的方程;
(Ⅱ)求过点A(2,6)且被圆C:(x﹣3)2+(y﹣4)2=4截得的弦长为![]() 的直线l的方程.
的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com