
【题目】若![]() ,m 是两条不同的直线,m 垂直于平面
,m 是两条不同的直线,m 垂直于平面![]() ,则“
,则“![]() ”是“
”是“![]() " 的 ( )
" 的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】B
【解析】若![]() ,因为m垂直平面
,因为m垂直平面![]() ,则
,则![]() 或
或![]() ,又m垂直于平面
,又m垂直于平面![]() ,则
,则![]() ,所以“
,所以“![]() ”是
”是![]() 的必要不充分条件,故选B。
的必要不充分条件,故选B。
【考点精析】利用空间点、线、面的位置和空间点、线、面的位置对题目进行判断即可得到答案,需要熟知如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线);(平行线的传递性)平行与同一直线的两条直线互相平行;如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线);(平行线的传递性)平行与同一直线的两条直线互相平行.


科目:高中数学 来源: 题型:
【题目】某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1 , 设AB1的中点为D,B1CB![]() C1=E.求证:
C1=E.求证: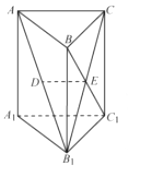
(1)DE∥平面AA1C1C
(2)BC1⊥AB1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球A1, A2和1个白球B的甲箱与装有2个红球a1,a2和2个白球b1,b2的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(1)用球的标号列出所有可能的摸出结果;
(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)过点(0,
(a>b>0)过点(0,![]() ),且离心率为
),且离心率为![]() 。
。
(Ⅰ)求椭圆E的方程;
(II)设直线x my 1,(m R)交椭圆E与A,B两点,判断点G(-![]() ,0)与以线段AB为直径的圆的位置关系,并说明理由。
,0)与以线段AB为直径的圆的位置关系,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() 在其定义域内都存在唯一的
在其定义域内都存在唯一的![]() 使
使![]() 成立,则称该函数为“依赖函数”.
成立,则称该函数为“依赖函数”.
(1)判断函数![]() 是否为“依赖函数”,并说明理由;
是否为“依赖函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上为“依赖函数”,求实数
上为“依赖函数”,求实数![]() 乘积
乘积![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依赖函数”,若存在实数
上为“依赖函数”,若存在实数![]() 使得对任意的
使得对任意的![]() 有不等式
有不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com