
ЁОЬтФПЁПФГПЭЛЇПМВьСЫвЛПюШШЯњЕФОЛЫЎЦїЃЌЪЙгУЪйУќЮЊЪЎФъЃЌЙ§ТЫгЩКЫаФВПМўТЫаОРДЪЕЯж.дкЪЙгУЙ§ГЬжаЃЌТЫаОашвЊВЛЖЈЦкИќЛЛЃЌЦфжаТЫаОУПИі200дЊ.ШчЭМЪЧИљОн100ЬЈИУПюОЛЫЎЦїдкЪЎФъЪЙгУЦкФкИќЛЛЕФТЫаОЕФМўЪ§жЦГЩЕФжљзДЭМ.ЃЈвд100ЬЈОЛЫЎЦїИќЛЛТЫаОЕФЦЕТЪДњЬц1ЬЈОЛЫЎЦїИќЛЛТЫаОЗЂЩњЕФИХТЪЃЉ
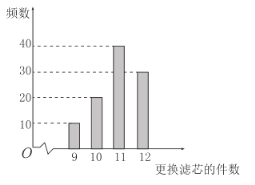
ЃЈ1ЃЉЙРМЦвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§ЕФжкЪ§КЭжаЮЛЪ§.
ЃЈ2ЃЉЙРМЦвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§Дѓгк10ЕФИХТЪ.
ЃЈ3ЃЉвбжЊЩЯЪі100ЬЈОЛЫЎЦїдкЙКЛњЕФЭЌЪБЙКТђТЫаОЯэЪм5елгХЛнЃЈЪЙгУЙ§ГЬжаШчашдйЙКТђЮогХЛнЃЉЃЌМйЩшУПЬЈОЛЫЎЦїдкЙКЛњЕФЭЌЪБЙКТђТЫаО10ИіЃЌет100ЬЈОЛЫЎЦїдкЪЙгУЦкФкЃЌИќЛЛТЫаОЕФМўЪ§МЧЮЊaЃЌЫљашЗбгУМЧЮЊyЃЌВЙШЋЯТБэЃЌЙРМЦет100ЬЈОЛЫЎЦїдкЪЙгУЦкФкЙКТђТЫаОЫљашзмЗбгУЕФЦНОљЪ§.
100ЬЈИУПюОЛЫЎЦїдкЪдгУЦкФкИќЛЛТЫаОЕФМўЪ§a | 9 | 10 | 11 | 12 |
ЦЕЪ§ | ||||
ЗбгУy |
ЁОД№АИЁПЃЈ1ЃЉжкЪ§ЮЊ11ЃЌжаЮЛЪ§ЮЊ11ЃЛЃЈ2ЃЉ0.7ЃЛЃЈ3ЃЉМћНтЮіЃЌ1200дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬѕаЮЭМЙРМЦвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§ЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ2ЃЉЯШЧѓГівЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§Дѓгк10ЕФЦЕЪ§ЮЊ70ЃЈЬЈЃЉЃЌдйРћгУЙХЕфИХаЭЕФИХТЪЙЋЪНЕУНтЃЛ
ЃЈ3ЃЉЯШЭЈЙ§МЦЫуЕУЕНЖдгІЕФЗбгУy,дйРћгУЦНОљЪ§ЕФЙЋЪНЧѓНт.
ЃЈ1ЃЉЙРМЦвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§ЕФжкЪ§ЮЊ11.
ЙРМЦвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§ЕФжаЮЛЪ§ЮЊ11.
ЃЈ2ЃЉвђЮЊдк100ЬЈОЛЫЎЦїжаЃЌвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§Дѓгк10ЕФЦЕЪ§ЮЊ![]() ЃЈЬЈЃЉЃЌ
ЃЈЬЈЃЉЃЌ
ЫљвдЃЌвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§Дѓгк10ЕФЦЕТЪЮЊ![]() .
.
ЙЪЙРМЦвЛЬЈОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§Дѓгк10ЕФИХТЪЮЊ0.7.
ЃЈ3ЃЉ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
![]() ЪБЃЌ
ЪБЃЌ![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
![]() ЪБЃЌ
ЪБЃЌ![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
![]() ЪБЃЌ
ЪБЃЌ![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
ВЙШЋБэИёЕУЃК
100ЬЈИУПюОЛЫЎЦїдкЪЙгУЦкФкИќЛЛТЫаОЕФМўЪ§a | 9 | 10 | 11 | 12 |
ЦЕТЪ | 0.1 | 0.2 | 0.4 | 0.3 |
ЗбгУy | 1000 | 1000 | 1200 | 1400 |
МйЩшУПЬЈОЛЫЎЦїЙКТђвЛМЖТЫаО10ИіЃЌдђет100ЬЈОЛЫЎЦїдкЪЙгУЦкФкЙКТђТЫаОЫљашзмЗбгУЕФЦНОљЪ§ЮЊ![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЛБіЫЙЛљШ§НЧаЮЪЧвЛжжЗжаЮЃЌгЩВЈРМЪ§бЇМваЛБіЫЙЛљдк1915ФъЬсГіЃЌЯШзївЛИіе§Ш§НЧаЮЃЎЭкШЅвЛИіЁАжааФШ§НЧаЮЁБЃЈМДвддШ§НЧаЮИїБпЕФжаЕуЮЊЖЅЕуЕФШ§НЧаЮЃЉЃЌШЛКѓдкЪЃЯТЕФаЁШ§НЧаЮжагжЭкШЅвЛИіЁАжааФШ§НЧаЮЁБЃЌЮвУЧгУАзЩЋДњБэЭкШЅЕФУцЛ§ЃЌФЧУДКкШ§НЧаЮЮЊЪЃЯТЕФУцЛ§ЃЈЮвУЧГЦКкШ§НЧаЮЮЊаЛБіЫЙЛљШ§НЧаЮЃЉЃЎЯђЭМжаЕк5ИіДѓе§Ш§НЧаЮжаЫцЛњШі512СЃДѓаЁОљдШЕФЯИаЁПХСЃЮяЃЌдђТфдкАзЩЋЧјгђЕФЯИаЁПХСЃЮяЕФЪ§СПдМЪЧЃЈ ЃЉ

A.256B.350C.162D.96
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЪ§Са![]() ЁЂ
ЁЂ![]() ЃЌАбКЭ
ЃЌАбКЭ![]() НазіЪ§Са
НазіЪ§Са![]() гы
гы![]() ЕФЧА
ЕФЧА![]() ЯюЗККЭЃЌМЧзїЮЊ
ЯюЗККЭЃЌМЧзїЮЊ![]() .вбжЊЪ§Са
.вбжЊЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЧв
ЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЪ§Са![]() гыЪ§Са
гыЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюЕФЗККЭЮЊ
ЯюЕФЗККЭЮЊ![]() ЃЌЧв
ЃЌЧв![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉДгЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюжаЃЌШЮШЁ
ЯюжаЃЌШЮШЁ![]() ЯюДгаЁЕНДѓвРДЮХХСаЃЌЕУЕНЪ§Са
ЯюДгаЁЕНДѓвРДЮХХСаЃЌЕУЕНЪ§Са![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЛдйНЋгрЯТЕФ
ЃЛдйНЋгрЯТЕФ![]() ЯюДгДѓЕНаЁвРДЮХХСаЃЌЕУЕНЪ§Са
ЯюДгДѓЕНаЁвРДЮХХСаЃЌЕУЕНЪ§Са![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() .ЧѓЪ§Са
.ЧѓЪ§Са![]() гыЪ§Са
гыЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюЕФЗККЭ
ЯюЕФЗККЭ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() гыЫФБпаЮ
гыЫФБпаЮ![]() ЖМЪЧжБНЧЬнаЮЃЌ
ЖМЪЧжБНЧЬнаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊСтаЮЃЌ
ЮЊСтаЮЃЌ![]() ЃЎ
ЃЎ
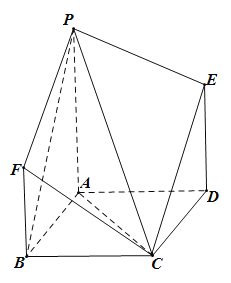
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌ![]() ЪЧвд
ЪЧвд![]() ЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌ![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ![]() ЃЌШчЭМЂкЃЌНЋ
ЃЌШчЭМЂкЃЌНЋ![]() би
би![]() елЦ№ЪЙЦНУц
елЦ№ЪЙЦНУц![]() ЦНУц
ЦНУц![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкРт
дкРт![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() дкРт
дкРт![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() .
.
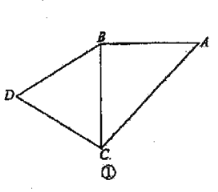
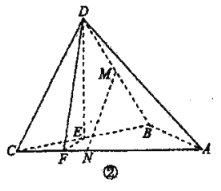
ЃЈ1ЃЉдкРт![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙЦНУц
ЃЌЪЙЦНУц![]() ЦНУц
ЦНУц![]() ЃПШєДцдкЃЌЧѓ
ЃПШєДцдкЃЌЧѓ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ2ЃЉЧѓЕу![]() ЕНЦНУц
ЕНЦНУц![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнЁЖШЫУёЭјЁЗБЈЕРЃЌУРЙњЙњМвКНПеКНЬьОжЃЈNASAЃЉЗЂЮФГЦЃЌЯрБШ20ФъЧАЪРНчБфЕУИќТЬЩЋСЫЃЌЮРаЧзЪСЯЯдЪОжаЙњКЭгЁЖШЕФааЖЏжїЕМСЫЕиЧђБфТЬ.ОнЭГМЦЃЌжаЙњаТдіТЬЛЏУцЛ§ЕФ![]() РДздгкжВЪїдьСжЃЌЯТБэЪЧжаЙњЪЎИіЕиЧјдкШЅФъжВЪїдьСжЕФЯрЙиЪ§Он.ЃЈдьСжзмУцЛ§ЮЊШЫЙЄдьСжЁЂЗЩВЅдьСжЁЂаТЗтЩНг§СжЁЂЭЫЛЏСжаоИДЁЂШЫЙЄИќаТЕФУцЛ§жЎКЭЃЉ
РДздгкжВЪїдьСжЃЌЯТБэЪЧжаЙњЪЎИіЕиЧјдкШЅФъжВЪїдьСжЕФЯрЙиЪ§Он.ЃЈдьСжзмУцЛ§ЮЊШЫЙЄдьСжЁЂЗЩВЅдьСжЁЂаТЗтЩНг§СжЁЂЭЫЛЏСжаоИДЁЂШЫЙЄИќаТЕФУцЛ§жЎКЭЃЉ
ЕЅЮЛЃКЙЋЧъ
ЕиЧј | дьСжзмУцЛ§ | дьСжЗНЪН | ||||
ШЫЙЄдьСж | ЗЩВЅдьСж | аТЗтЩНг§Сж | ЭЫЛЏСжаоИД | ШЫЙЄИќаТ | ||
ФкУЩ | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
КгББ | 583361 | 345625 | 33333 | 13507 | 65653 | 3643 |
КгФЯ | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
жиЧь | 226333 | 100600 | 62400 | 63333 | ||
ЩТЮї | 297642 | 184108 | 33602 | 63865 | 16067 | |
ИЪЫр | 325580 | 260144 | 57438 | 7998 | ||
аТНЎ | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
ЧрКЃ | 178414 | 16051 | 159734 | 2629 | ||
ФўЯФ | 91531 | 58960 | 22938 | 8298 | 1335 | |
ББОЉ | 19064 | 10012 | 4000 | 3999 | 1053 | |
ЃЈ1ЃЉЧыИљОнЩЯЪіЪ§ОнЗжБ№аДГідкетЪЎИіЕиЧјжаШЫЙЄдьСжУцЛ§гыдьСжзмУцЛ§ЕФБШжЕзюДѓКЭзюаЁЕФЕиЧјЃЛ
ЃЈ2ЃЉдкетЪЎИіЕиЧјжаЃЌШЮбЁвЛИіЕиЧјЃЌЧѓИУЕиЧјаТЗтЩНг§СжУцЛ§еМдьСжзмУцЛ§ЕФБШжЕГЌЙ§![]() ЕФИХТЪЃЛ
ЕФИХТЪЃЛ
ЃЈ3ЃЉдкетЪЎИіЕиЧјжаЃЌДгЭЫЛЏСжаоИДУцЛ§ГЌЙ§вЛЭђЙЋЧъЕФЕиЧјжаЃЌШЮбЁСНИіЕиЧјЃЌМЧXЮЊетСНИіЕиЧјжаЭЫЛЏСжаоИДУцЛ§ГЌЙ§СљЭђЙЋЧъЕФЕиЧјЕФИіЪ§ЃЌЧѓXЕФЗжВМСаМАЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНЬхABCDЉA1B1C1D1жаЃЌEЮЊD1DЕФжаЕуЃЌACгыBDЕФНЛЕуЮЊOЃЎ
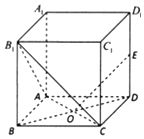
ЃЈ1ЃЉЧѓжЄЃКEOЁЭЦНУцAB1CЃЛ
ЃЈ2ЃЉдкгЩе§ЗНЬхЕФЖЅЕуШЗЖЈЕФЦНУцжаЃЌЪЧЗёДцдкгыЦНУцAB1CЦНааЕФЦНУцЃПжЄУїФуЕФНсТл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЪЧЖЈвхдкRЩЯЕФЦцКЏЪ§ЃЌЕБ
ЪЧЖЈвхдкRЩЯЕФЦцКЏЪ§ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌИјГіЯТСаУќЬтЃК
ЃЌИјГіЯТСаУќЬтЃК
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЂкКЏЪ§![]() га2ИіСуЕуЃЛ
га2ИіСуЕуЃЛ
Ђл![]() ЕФНтМЏЮЊ
ЕФНтМЏЮЊ![]() ЃЛ
ЃЛ
Ђм![]() ЃЌ
ЃЌ![]() ЃЌЖМга
ЃЌЖМга![]() .
.
ЦфжаецУќЬтЕФИіЪ§ЮЊЃЈ ЃЉ
A.4B.3C.2D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§![]() ЕФЭМЯѓЯђзѓЦНвЦ
ЕФЭМЯѓЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌШЛКѓзнзјБъВЛБфЃЌКсзјБъБфЮЊдРДЕФ
ИіЕЅЮЛЃЌШЛКѓзнзјБъВЛБфЃЌКсзјБъБфЮЊдРДЕФ![]() БЖЃЌЕУЕН
БЖЃЌЕУЕН![]() ЕФЭМЯѓЃЌЯТУцЫФИіНсТле§ШЗЕФЪЧЃЈ ЃЉ
ЕФЭМЯѓЃЌЯТУцЫФИіНсТле§ШЗЕФЪЧЃЈ ЃЉ
A. КЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЮЊдіКЏЪ§
ЩЯЮЊдіКЏЪ§
B. НЋКЏЪ§![]() ЕФЭМЯѓЯђгвЦНвЦ
ЕФЭМЯѓЯђгвЦНвЦ![]() ИіЕЅЮЛКѓЕУЕНЕФЭМЯѓЙигкдЕуЖдГЦ
ИіЕЅЮЛКѓЕУЕНЕФЭМЯѓЙигкдЕуЖдГЦ
C. Еу![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЭМЯѓЕФвЛИіЖдГЦжааФ
ЭМЯѓЕФвЛИіЖдГЦжааФ
D. КЏЪ§![]() дк
дк![]() ЩЯЕФзюДѓжЕЮЊ
ЩЯЕФзюДѓжЕЮЊ![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com