
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集为空集,求
的解集为空集,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用零点分类讨论法求不等式![]() 的解集;(2)由题得|x+1|-|x-a|<2a恒成立,再求出
的解集;(2)由题得|x+1|-|x-a|<2a恒成立,再求出![]() , 解不等式a+1<2a得解.
, 解不等式a+1<2a得解.
(1)当a=2时,不等式![]() ,即|x+1|-|x-2|>2,
,即|x+1|-|x-2|>2,
当![]() 时,原不等式可化为-x-1+x-2>2,即-3>2,此时原不等式无解;
时,原不等式可化为-x-1+x-2>2,即-3>2,此时原不等式无解;
当![]() 时,原不等式可化为x+1+x-2>2,解得
时,原不等式可化为x+1+x-2>2,解得![]() ,所以
,所以![]() ;
;
当x>2时,原不等式可化为x+1-x+2>2,即3>2,此时原不等式恒成立,
所以x>2;
综上,原不等式的解集为![]() .
.
(2)由![]() 的解集为空集得
的解集为空集得![]() 的解集为空集,
的解集为空集,
所以|x+1|-|x-a|<2a恒成立.
因为![]() ,所以
,所以![]() ,
,
所以当且仅当![]() 即
即![]() 时,
时,![]() ,
,
所以a+1<2a,
解得a>1,
即![]() 的取值范围为
的取值范围为![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,下面五个命题:
,下面五个命题:
①对任意实数![]() 与
与![]() ,直线
,直线![]() 和圆
和圆![]() 有公共点;
有公共点;
②存在实数![]() 与
与![]() ,直线
,直线![]() 和圆
和圆![]() 相切;
相切;
③存在实数![]() 与
与![]() ,直线
,直线![]() 和圆
和圆![]() 相离;
相离;
④对任意实数![]() ,必存在实数
,必存在实数![]() ,使得直线
,使得直线![]() 与和圆
与和圆![]() 相切;
相切;
⑤对任意实数![]() ,必存在实数
,必存在实数![]() ,使得直线
,使得直线![]() 与和圆
与和圆![]() 相切.
相切.
其中真命题的代号是______________________(写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 在圆内,在过点P所作的圆的所有弦中,弦长最小值为
在圆内,在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
(1)求实数a的值;
(2)若点M为圆外的动点,过点M向圆C所作的两条切线始终互相垂直,求点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是古希腊数学家阿基米德用平衡法求球的体积所用的图形.此图由正方形![]() 、半径为
、半径为![]() 的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与
的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与![]() 的中点
的中点![]() 重合,斜边在直线
重合,斜边在直线![]() 上.已知
上.已知![]() 为
为![]() 的中点,现将该图形绕直线
的中点,现将该图形绕直线![]() 旋转一周,则阴影部分旋转后形成的几何体积为( )
旋转一周,则阴影部分旋转后形成的几何体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
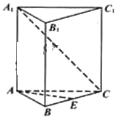
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Serum Drug Concentration)是指药物吸收后在血浆内的总浓度(单位:mg/ml),通常用血药浓度来研究药物的作用强度.下图为服用同等剂量的三种新药后血药浓度的变化情况,其中点![]() 的横坐标表示服用第
的横坐标表示服用第![]() 种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点
种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点![]() 的纵坐标表示第
的纵坐标表示第![]() 种药的血药浓度的峰值.(
种药的血药浓度的峰值.(![]() )
)

①记![]() 为服用第
为服用第![]() 种药后达到血药浓度峰值时,血药浓度提高的平均速度,则
种药后达到血药浓度峰值时,血药浓度提高的平均速度,则![]() 中最大的是_______;
中最大的是_______;
②记![]() 为服用第
为服用第![]() 种药后血药浓度从峰值降到峰值的一半所用的时间,则
种药后血药浓度从峰值降到峰值的一半所用的时间,则![]() 中最大的是_______
中最大的是_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为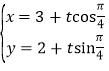 (其中
(其中![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系,并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com