
【题目】已知椭圆![]() 的左,右焦点分别是
的左,右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 被椭圆C截得的线段长为
被椭圆C截得的线段长为![]() .
.
(1)求椭圆C的方程;
(2)过点![]() 且斜率为k的直线l交椭圆C于A,B两点,交x轴于P点,点A关于x轴的对称点为M,直线BM交x轴于Q点.求证:
且斜率为k的直线l交椭圆C于A,B两点,交x轴于P点,点A关于x轴的对称点为M,直线BM交x轴于Q点.求证:![]() (O为坐标原点)为常数.
(O为坐标原点)为常数.
科目:高中数学 来源: 题型:
【题目】新中国昂首阔步地走进2019年,迎来了她70岁华诞.某平台组织了“伟大的复兴之路一新中国70周年知识问答”活动,规则如下:共有30道单选题,每题4个选项中只有一个正确,每答对一题获得5颗红星,每答错一题反扣2颗红星;若放弃此题,则红星数无变化.答题所获得的红星可用来兑换神秘礼品,红星数越多奖品等级越高.小强参加该活动,其中有些题目会做,有些题目可以排除若干错误选项,其余的题目则完全不会.
(1)请问:对于完全不会的题目,小强应该随机从4个选项中选一个作答,还是选择放弃?(利用统计知识说明理由)
(2)若小强有12道题目会做,剩下的题目中,可以排除一个错误选项、可以排除两个错误选项和完全不会的题目的数量比是![]() .请问:小强在本次活动中可以获得最多红星数的期望是多少?
.请问:小强在本次活动中可以获得最多红星数的期望是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为
的最小值为![]() ,
,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象关于原点对称.
的图象关于原点对称.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现计划用两张铁丝网在一片空地上围成一个梯形养鸡场![]() ,
,![]() ,
,![]() ,已知
,已知![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成,
的铁丝网折成,![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成.设上底
的铁丝网折成.设上底![]() 的长为
的长为![]() ,所围成的梯形面积为
,所围成的梯形面积为![]() .
.
(1)求S关于x的函数解析式,并求x的取值范围;
(2)当x为何值时,养鸡场的面积最大?最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )
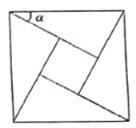
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com