
【题目】某中学校本课程开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生.
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数ξ的分布列及数学期望.
【答案】
(1)解:每个学生有四个不同的选择,
根据分步乘法计数原理,
这3名学生选修课所有选法的总数N=4×4×4=64
(2)解:恰有2门选修课这3名学生都没选择的概率为:
![]() =
= ![]() =
= ![]()
(3)解:A选修课被这3名学生选择的人数为ξ,则ξ的可能取值为0,1,2,3,
P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =
= ![]()
【解析】(1)每个学生有四个不同的选择,由此根据分步乘法计数原理,能求出这3名学生选修课所有选法的总数.(2)由已知利用排列组合知识能求出恰有2门选修课这3名学生都没选择的概率.(3)A选修课被这3名学生选择的人数为ξ,则ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆方程:
(1)长轴在x轴上,长轴长等于12,离心率等于 ![]() ;
;
(2)椭圆经过点(﹣6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人 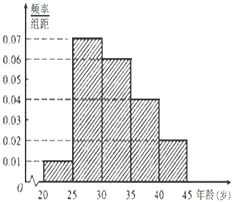
(1)求该组织的人数;
(2)若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中: ①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )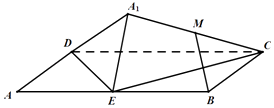
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com