
分析 (1)a1=1,an+1=3an+2n(n∈N*),变形为an+1+2n+1=3(an+2n),a1+2=3,利用等比数列的通项公式即可得出.
(2)由bn=$\frac{n}{{2}^{n-1}}$利用“错位相减法”与等比数列的求和公式可得:Tn=4-$\frac{2+n}{{2}^{n-1}}$.不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$化为:(-1)nλ<4-$\frac{2}{{2}^{n-1}}$,通过分类讨论利用数列的单调性即可得出.
(3)3n=(2+1)n=2n+${∁}_{n}^{1}$×2+${∁}_{n}^{2}×{2}^{2}$+…+1,可得$\frac{1}{{a}_{n}}$=$\frac{1}{{3}^{n}-{2}^{n}}$≤$\frac{1}{2{n}^{2}}$<$\frac{1}{2(n-1)n}$=$\frac{1}{2}(\frac{1}{n-1}-\frac{1}{n})$(n≥2).再利用“裂项求和”方法、数列的单调性即可得出.
解答 (1)证明:∵a1=1,an+1=3an+2n(n∈N*),∴an+1+2n+1=3(an+2n),a1+2=3.∴{an+2n}是等比数列,公比为3,首项为3.
∴an+2n=3n,∴an=3n-2n.
(2)解:∵bn=$\frac{n}{{2}^{n-1}}$,∴数列{bn}前n项和为Tn=1+$\frac{2}{2}$+$\frac{3}{{2}^{2}}$+…+$\frac{n}{{2}^{n-1}}$,
∴$\frac{1}{2}$Tn=$\frac{1}{2}+\frac{2}{{2}^{2}}$+…+$\frac{n-1}{{2}^{n-1}}$+$\frac{n}{{2}^{n}}$,
∴$\frac{1}{2}$Tn=1+$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{n}{{2}^{n}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n}}$,
∴Tn=4-$\frac{2+n}{{2}^{n-1}}$.
不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$化为:(-1)nλ<4-$\frac{2}{{2}^{n-1}}$,
当n=2k-1(k∈N*)时,化为:-λ<4-$\frac{2}{{2}^{n-1}}$,∴-λ<2,解得λ>-2.
当n=2k(k∈N*)时,化为:λ<4-$\frac{2}{{2}^{n-1}}$,∴λ<32.
∵不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*恒成立,∴-2<λ<3.
(3)证明:∵3n=(2+1)n=2n+${∁}_{n}^{1}$×2+${∁}_{n}^{2}×{2}^{2}$+…+1.
$\frac{1}{{a}_{n}}$=$\frac{1}{{3}^{n}-{2}^{n}}$≤$\frac{1}{2{n}^{2}}$<$\frac{1}{2(n-1)n}$=$\frac{1}{2}(\frac{1}{n-1}-\frac{1}{n})$(n≥2).
∴对一切正整数n,有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<1+$\frac{1}{2}[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})]$=1+$\frac{1}{2}(1-\frac{1}{n})$=$\frac{3}{2}$-$\frac{1}{2n}$<$\frac{3}{2}$.
∴对一切正整数n,有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<$\frac{3}{2}$.
点评 本题考查了等比数列的通项公式及其求和公式、“错位相减法”、“裂项求和”方法、数列的单调性、二项式定理的应用,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C为圆O上三点,点B平分弧$\widehat{AC}$,点P为AC延长线上一点,PQ是圆O的切线,切点为Q,BQ与AC相交于点D.
如图,A,B,C为圆O上三点,点B平分弧$\widehat{AC}$,点P为AC延长线上一点,PQ是圆O的切线,切点为Q,BQ与AC相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
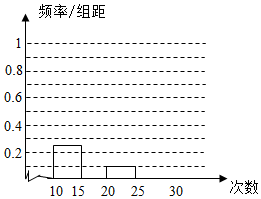 对某校高一学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数与频率的统计表和频率分布直方图.
对某校高一学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 24 | n |
| [20,25) | 4 | 0.10 |
| [25,30) | m | p |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com