
����Ŀ����ͼ��ˮƽ���õ����������β����������������̨�β���������ĸ߾�Ϊ32cm��������ĵ���Խ���AC�ij�Ϊ10![]() cm���������������Խ���
cm���������������Խ���![]() ��
��![]() �ij��ֱ�Ϊ14cm��62cm���ֱ������������������ע��ˮ��ˮ���Ϊ12cm������һ��������l���䳤��Ϊ40cm����������ȡ���������ϸ�����Բ��ƣ�
�ij��ֱ�Ϊ14cm��62cm���ֱ������������������ע��ˮ��ˮ���Ϊ12cm������һ��������l���䳤��Ϊ40cm����������ȡ���������ϸ�����Բ��ƣ�
��1����![]() ��������������
��������������![]() ��һ�����ڵ�A������һ�����ڲ���
��һ�����ڵ�A������һ�����ڲ���![]() �ϣ���
�ϣ���![]() û��ˮ�в��ֵij��ȣ�
û��ˮ�в��ֵij��ȣ�
��2����![]() ��������������
��������������![]() ��һ�����ڵ�E������һ�����ڲ���
��һ�����ڵ�E������һ�����ڲ���![]() �ϣ���
�ϣ���![]() û��ˮ�в��ֵij��ȣ�
û��ˮ�в��ֵij��ȣ�
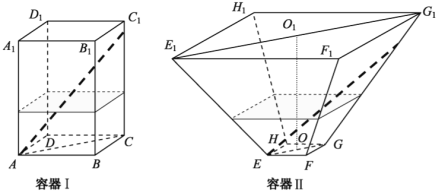
��������1��16����2��20��
����������˼·��������1��ת��Ϊֱ��������ACM�У����������������AP1����2��ת����������EGN�У�������ֱ�������������![]() �����������Ҷ������
�����������Ҷ������![]() ��������ֱ����������ߣ���Ϊ
��������ֱ����������ߣ���Ϊ![]() û��ˮ�в��ֵij��ȣ�
û��ˮ�в��ֵij��ȣ�
��1�����������Ķ��壬![]() ƽ��
ƽ��![]() ������ƽ��
������ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��
�Dz���������һ������![]() �ϵ�
�ϵ�![]() ����
����
��Ϊ![]() ������
������![]() ���Ӷ�
���Ӷ�![]() ��
��
��ͼ��![]() ��ˮ�������Ϊ
��ˮ�������Ϊ![]() ����
����![]() ��P1Q1��AC��Q1Ϊ���㣬
��P1Q1��AC��Q1Ϊ���㣬
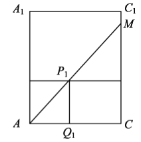
��P1Q1��ƽ��ABCD����P1Q1=12���Ӷ�AP1=![]() ��
��
�𣺲�����lû��ˮ�в��ֵij���Ϊ16cm����5�֣�
(�������û��ˮ�в���������Ϊ��ˮ�����ϲ�����������Ϊ24cm)
��2����ͼ��O��O1������̨�����������ģ�
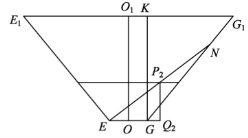
������̨�Ķ��壬OO1��ƽ��EFGH������ƽ��E1EGG1��ƽ��EFGH��O1O��EG��
ͬ����ƽ��E1EGG1��ƽ��E1F1G1H1��O1O��E1G1��
�Dz���������һ������GG1�ϵ�N����
��G��GK��E1G1��KΪ���㣬��GK =OO1=32��
��ΪEG = 14��E1G1= 62��
����KG1=![]() ���Ӷ�
���Ӷ�![]() ��
��
��![]() ��
��![]() ��
��
��Ϊ![]() ������
������![]() ��
��
��![]() �У������Ҷ����ɵ�
�У������Ҷ����ɵ�![]() �����
�����![]() ��
��
��Ϊ![]() ������
������![]() ��
��
����![]() ��
��
��EN��ˮ��Ľ���ΪP2����P2��P2Q2��EG��Q2Ϊ���㣬��P2Q2��ƽ��EFGH��
��P2Q2=12���Ӷ�EP2=![]() ��
��
�𣺲�����lû��ˮ�в��ֵij���Ϊ20cm����10�֣�
(�������û��ˮ�в���������Ϊ��ˮ�����ϲ�����������Ϊ20cm)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵ���ֱ��������![]() �У�
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ��
��![]() ����
����![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() .
.
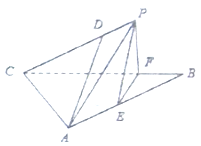
(1)��֤�� ![]() ƽ��
ƽ��![]() ��
��
(2)������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() ��
��![]() �ĵ�����.
�ĵ�����.
��1����![]() �ļ�ֵ��
�ļ�ֵ��
��2��֤����������ʵ��![]() ������
������![]() �������
�������
��3����![]() ��
��![]() ʱ���������ʵ��
ʱ���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������4���˲μ�ij���ֻ���û�мס���������Ϸ�ɹ��μ���ѡ��Ϊ����Ȥζ�ԣ�Լ����ÿ����ͨ����һö�ʵؾ��ȵ����Ӿ����Լ�ȥ�μ��ĸ���Ϸ����������Ϊ1��2����ȥ�μӼ���Ϸ��������������2����ȥ�μ�����Ϸ��
��1�� ���4������ǡ��2����ȥ �μӼ���Ϸ�ĸ��ʣ�
��2������4������ȥ�μӼ���Ϸ��������ȥ�μ�����Ϸ�������ĸ��ʣ�
��3����![]() �ֱ��ʾ��4������ȥ�μӼס�����Ϸ����������
�ֱ��ʾ��4������ȥ�μӼס�����Ϸ����������![]() ,���������
,���������![]() �ķֲ�������ѧ����
�ķֲ�������ѧ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ΪP(kg)�Ļ���ʱ������ÿǧ�ķ���(��λ��Ԫ)��Ϊ��
y=![]()
�Ա�дһ�������������˷�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��ֱ��
��ֱ��![]() ��б����
��б����![]() �ҹ�������
�ҹ�������![]() �Ľ��㣬ֱ��
�Ľ��㣬ֱ��![]() ��������
��������![]() �صõ��߶γ���16��˫����
�صõ��߶γ���16��˫����![]() ��
�� ![]() ��һ��������������
��һ��������������![]() �����ϣ���ֱ��
�����ϣ���ֱ��![]() ��
��![]() ��Ľ���
��Ľ���![]() ��˫����
��˫����![]() ��һ�������ߵľ����ǣ� ��
��һ�������ߵľ����ǣ� ��
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ԡ���ɫ���С�Ϊ��ּ��չ������������ҵ��.�õ���ij����ѧһ��ȤС����20���߶���ѧ����15����һ��ѧ����ɣ��ֲ��÷ֲ�����ķ�����ȡ7�ˣ����һ������С��ȥ�г����顰������������ʹ��.�ʣ�
����Ӧ�Ӹ���ȤС���г�ȡ��һ���߶�����ѧ���������ˣ�
������֪�õ�����![]() ,
, ![]() �����ͺŵġ����������������г������У�������С��ĸ߶���ѧ������
�����ͺŵġ����������������г������У�������С��ĸ߶���ѧ������![]() �ͳ�����һ��ѧ������
�ͳ�����һ��ѧ������![]() �ͳ�.
�ͳ�.
��1����������������ȡ3�ˣ����ȡ��3����������2�����г������������![]() �ͳ��ĸ���;
�ͳ��ĸ���;
��2����֪�õ���![]() �ͳ�ÿСʱ�����Ϊ1Ԫ��
�ͳ�ÿСʱ�����Ϊ1Ԫ�� ![]() �ͳ�ÿСʱ�����Ϊ1.2Ԫ����
�ͳ�ÿСʱ�����Ϊ1.2Ԫ����![]() Ϊ������С���������ȡ3�˵õ���ÿСʱ���֮�ͣ���
Ϊ������С���������ȡ3�˵õ���ÿСʱ���֮�ͣ���![]() ����ѧ����.
����ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|x2��6x+8��0}��B={x|��x��a����x��3a����0}��
��1����a=1����A��B��
��2����A��B=����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ�����Զ�����ҹ�²��С��ij�����ڴ���Ʒ�ַ�ѿ����֮��Ĺ�ϵ���з����о������Ƿֱ��¼��12��1����12��5�յ�ÿ����ҹ�²���ʵ����ÿ��ÿ100�������еķ�ѿ�����õ��������ϣ�
�� �� | 12��1�� | 12��2�� | 12��3�� | 12��4�� | 12��5�� |
�²� | 10 | 11 | 13 | 12 | 8 |
��ѿ�� | 23 | 25 | 30 | 26 | 16 |
��ũ����ȷ�����о�������:�ȴ�������������ѡȡ2�飬��ʣ�µ�3�����������Իع鷽�̣��ٶԱ�ѡȡ��2�����ݽ��м��飮
��1����ѡȡ��2������ǡ���Dz�����2�����ݵĸ��ʣ�
��2����ѡȡ����12��1����12��5�յ��������ݣ������12��2����12��4�յ����ݣ����y����x�����Իع鷽��![]() ��
��
��3���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ����ʣ�2�������õ����Իع鷽���Ƿ�ɿ���
��ע�� 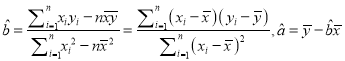 ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com