
分析 (1)由条件利用绝对值的意义求得f(x)的最小值,从而求得实数m的最小值M.
(2)由题意可得即 $\frac{3a+b}{4}$=1,故有 $\frac{3}{b}$+$\frac{1}{a}$=$\frac{\frac{3(3a+b)}{4}}{b}$+$\frac{\frac{3a+b}{4}}{a}$=$\frac{3}{2}$+$\frac{9a}{4b}$+$\frac{b}{4a}$,再利用基本不等式证得$\frac{3}{b}$+$\frac{1}{a}$≥3.
解答 解:函数f(x)=|x-3|-|x+2|表述数轴上的x的对应点到3对应点的距离减去它到-2对应点的距离,
它的最小值为-5,最大值为5,
(1)若不等式f(x)≥|m-1|有解,则5≥|m-1|,即-5≤m-1≤5,求得-4≤m≤6,故实数m的最小值M=-4.
(2)在(1)的条件下,若正数a,b满足3a+b=-M=4,即 $\frac{3a+b}{4}$=1,
∴$\frac{3}{b}$+$\frac{1}{a}$=$\frac{\frac{3(3a+b)}{4}}{b}$+$\frac{\frac{3a+b}{4}}{a}$=$\frac{3}{2}$+$\frac{9a}{4b}$+$\frac{b}{4a}$≥$\frac{3}{2}$+2$\sqrt{\frac{9a}{4b}•\frac{b}{4a}}$+3=$\frac{3}{2}$+2•$\frac{3}{4}$=3,
即 $\frac{3}{b}$+$\frac{1}{a}$≥3.
点评 本题主要考查绝对值的意义,函数的能成立问题,基本不等式的应用,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | {2,6} | B. | {1,5} | C. | {1,6} | D. | {5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
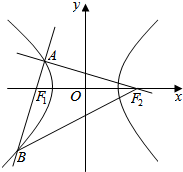 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )| A. | $\sqrt{5+2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{4-2\sqrt{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R使得2${\;}^{{x}_{0}}$>0 | B. | 存在x0∈R使得2${\;}^{{x}_{0}}$>0 | ||
| C. | 对任意x∈R,2x>0 | D. | 对任意x∈R,2x≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
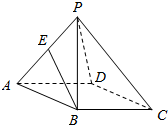 如图,在底面为正方形的四棱锥P-ABCD中,PA=PB=PC=PD=AB=2,点E为棱PA的中点,则异面直线BE与PD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,在底面为正方形的四棱锥P-ABCD中,PA=PB=PC=PD=AB=2,点E为棱PA的中点,则异面直线BE与PD所成角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com