
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(2)是否存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立?若存在,求出
成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】如图,圆柱体木材的横截面半径为![]() ,从该木材中截取一段圆柱体,再加工制作成直四棱柱
,从该木材中截取一段圆柱体,再加工制作成直四棱柱![]() ,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心
,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心![]() 在梯形
在梯形![]() 内部,
内部,![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
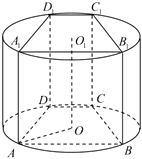
(1)求梯形![]() 的面积;
的面积;
(2)当![]() 取何值时,直四棱柱
取何值时,直四棱柱![]() 的体积最大?并求出最大值(注:木材的长度足够长)
的体积最大?并求出最大值(注:木材的长度足够长)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ABE﹣DCF和一个四棱锥P﹣ABCD组合而成,其中EF=EA=EB=2,AE⊥EB,PA=PD![]() ,平面PAD∥平面EBCF.
,平面PAD∥平面EBCF.
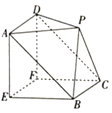
(1)证明:平面PBC∥平面AEFD;
(2)求直线AP与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,若
,每单提成4元,若![]() ,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若
,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
表1:美团外卖配送员甲送餐量统计
日送餐量x(单) | 13 | 14 | 16 | 17 | 18 | 20 |
天数 | 2 | 6 | 12 | 6 | 2 | 2 |
表2:饿了么外卖配送员乙送餐量统计
日送餐量x(单) | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)设美团外卖配送员月工资为![]() ,饿了么外卖配送员月工资为
,饿了么外卖配送员月工资为![]() ,当
,当![]() 时,比较
时,比较![]() 与
与![]() 的大小关系
的大小关系
(2)将4月份的日送餐量的频率视为日送餐量的概率
(ⅰ)计算外卖配送员甲和乙每日送餐量的数学期望E(X)和E(Y)
(ⅱ)请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,学校举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确给改选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() 的概率;
的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
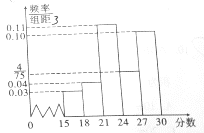
【题目】某中学为调查高三学生英语听力水平的情况,随机抽取了高三年级的80名学生进行测试,根据测试结果绘制了英语听力成绩(满分为30分)的频率分布直方图,将成绩不低于27分的定为优秀
(1)根据已知条件完成下面的![]() 列联表,并据此资料判断是否有90%的把握认为英语听力成绩是否优秀与性别有关?
列联表,并据此资料判断是否有90%的把握认为英语听力成绩是否优秀与性别有关?
英语听力优秀 | 非英语听力优秀 | 合计 | |
男同学 | 10 | ||
女同学 | 36 | ||
合计 |
(2)将上述调查所得到的频率视为概率,现在从该校高三学生中,采取随机抽样方法每次抽取1名学生,共抽取3次,记被抽取的3名学生中“英语听力优秀”的人数为X,若每次抽取的结果是相互独立的,求X的分布列和数学期望E(X)
参考公式: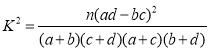 ,其中
,其中![]()
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com