
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有2人去淘宝网购物的概率;
(2)求这4个人中去淘宝网购物的人数大于去京东商城购物的人数的概率:
(3)用X,Y分别表示这4个人中去淘宝网购物的人数和去京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】为了了解某校九年级1 600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据直方图的数据,下列结论错误的是( )
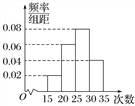
A. 该校九年级学生1分钟仰卧起坐的次数的中位数为26.25
B. 该校九年级学生1分钟仰卧起坐的次数的众数为27.5
C. 该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人
D. 该校九年级学生1分钟仰卧起坐的次数少于20次的约有32人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an=2+2cos2![]() ,n∈N*,等差数列{bn}满足a1=2b1,a2=b2.
,n∈N*,等差数列{bn}满足a1=2b1,a2=b2.
(1)求bn;
(2)记cn=a2n-1b2n-1+a2nb2n,求cn;
(3)求数列{anbn}前2n项和S2n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1(-c,0),F2(c,0),直线
的左、右焦点分别为F1(-c,0),F2(c,0),直线![]() 交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
(1)求椭圆E的标准方程与离心率;
(2)若直线l与椭圆E交于C,D两点,且P(2,2)是线段CD的中点,求直线l的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系和直角坐标系中,极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合,曲线
轴的非负半轴重合,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)判断曲线![]() 与曲线
与曲线![]() 的位置关系,若两曲线相交,求出两交点间的距离.
的位置关系,若两曲线相交,求出两交点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数![]() 有
有![]() ,已知
,已知![]() ,若一个各项均为正数的数列
,若一个各项均为正数的数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,则数列
项和,则数列![]() 中第18项
中第18项![]() ( )
( )
A. ![]() B. 9 C. 18 D. 36
B. 9 C. 18 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
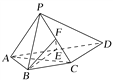
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com