练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．

    （Ⅰ）证明 PA//平面EDB；

    （Ⅱ）证明PB⊥平面EFD.

    【答案】(Ⅰ)详见解析；(Ⅱ)详见解析.

    【解析】

    （I）连结，交于．连结，通过中位线证明，由此证得平面.（2）先证得平面，由此证得，而，故平面，由此证得，结合，可证得平面.

    证明:（Ⅰ）连结，交于．连结．∵底面是正方形，∴点是的中点．在△中，是中位线，∴//．而平面，

    且平面，所以，//平面．

    （Ⅱ）∵⊥底面，且底面，∴⊥.

    ∵底面是正方形，有⊥,，平面，

    平面,∴⊥平面．而平面，∴⊥.

    又∵，是的中点，∴⊥，，

    平面，平面.∴⊥平面．而平面，

    ∴⊥．又⊥，且，平面，

    平面，所以⊥平面．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设是在点处的切线．

    （）求的解析式．

    （）求证： ．

    （）设，其中．若对恒成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

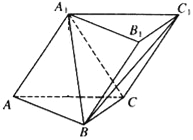
    【题目】如图，三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，AA1=A1C=AC=2，AB=BC且AB⊥BC，

    （Ⅰ）求证：AC⊥A1B；

    （Ⅱ）求二面角A﹣A1C﹣B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】交通拥堵指数是综合反映道路网畅通或拥堵的概念，记交通拥堵指数为 ，其范围为 ，分别有五个级别： 畅通； 基本畅通； 轻度拥堵； 中度拥堵； 严重拥堵．晚高峰时段 ，从某市交通指挥中心选取了市区 个交通路段，依据其交通拥堵指数数据绘制的直方图如图所示．

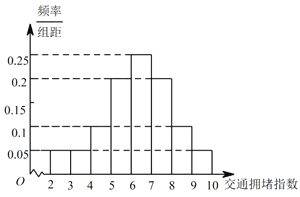
    （Ⅰ）求出轻度拥堵，中度拥堵，严重拥堵路段各有多少个；

    （Ⅱ）用分层抽样的方法从交通指数在 ， ， 的路段中共抽取个路段，求依次抽取的三个级别路段的个数；

    （Ⅲ）从（Ⅱ）中抽取的个路段中任取个，求至少个路段为轻度拥堵的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）当时，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，，其中，为自然对数的底数．

    （1）讨论的单调性；

    （2）证明：当时，；

    （3）确定的所有可能取值，使得在区间内恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组，…后，画出如下部分频率分布直方图.观察图形的信息，回答下列问题：

    （Ⅰ）求成绩落在上的频率，并补全这个频率分布直方图；

    （Ⅱ）估计这次考试的及格率（60分及以上为及格）和平均分；

    （Ⅲ）为调查某项指标，从成绩在60~80分，这两分数段组的学生中按分层抽样的方法抽取6人，再从这6人中选2人进行对比，求选出的这2名学生来自同一分数段的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊，无法确认，在图中经X表示。

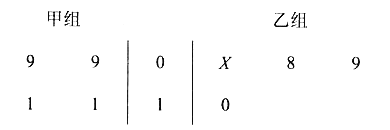
    （1）如果X=8，求乙组同学植树棵数的平均数和方差

    （2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的个数有（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    同步练习册答案