
【题目】已知动圆![]() 经过点
经过点![]() ,且动圆
,且动圆![]() 被
被![]() 轴截得的弦长为4,记圆心
轴截得的弦长为4,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)过![]() 轴下方一点
轴下方一点![]() 向曲线
向曲线![]() 作切线,切点记作
作切线,切点记作![]() 、
、![]() ,直线
,直线![]() 交曲线
交曲线![]() 于点
于点![]() ,若直线
,若直线![]() 、
、![]() 的斜率乘积为
的斜率乘积为![]() ,点
,点![]() 在以
在以![]() 为直径的圆上,求点
为直径的圆上,求点![]() 的坐标.
的坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量(单位:
(单位:分贝)与声音能量(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() =1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
=1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
| 45.7 |
|
| 0.51 |
|
| |||
| 5.1 | |||
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量的回归方程;
关于声音能量的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .己知点
.己知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: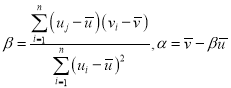 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数k的取值范围;
成立,求实数k的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 均相切,切点分别为
均相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于x的不等式
时,关于x的不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是偶函数,且当
是偶函数,且当![]() 时,
时,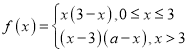
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)设函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试求
,试求![]() 的表达式;
的表达式;
(3)若方程![]() 有四个不同的实根,且它们成等差数列,试探求
有四个不同的实根,且它们成等差数列,试探求![]() 与
与![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
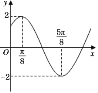
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝中华人民共和国成立70周年,2019年10月1日晚,金水桥南,百里长街成为舞台,3290名联欢群众演员跟着音乐的旋律,用手中不时变幻色彩的光影屏,流动着拼组出五星红旗、祖国万岁、长城等各式图案和文字.光影潋滟间,以《红旗颂》《我们走在大路上》《在希望的田野上》《领航新时代》四个章节,展现出中华民族从站起来、富起来到强起来的伟大飞跃.在每名演员的手中都有一块光影屏,每块屏有1024颗灯珠,若每个灯珠的开、关各表示一个信息,则每块屏可以表示出不同图案的个数为( )
A.2048B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com