
【题目】已知函数f(x)=﹣alnx+(a+1)x﹣![]() (a>0).
(a>0).
(1)讨论函数f(x)的单调性;
(2)若f(x)≥﹣![]() +ax+b恒成立,求a
+ax+b恒成立,求a![]() 时,实数b的最大值.
时,实数b的最大值.
【答案】(1)见解析;(2)![]()
【解析】
(1)求出![]() 并对其因式分解,对
并对其因式分解,对![]() 与1的大小分类讨论,由
与1的大小分类讨论,由![]() 的正负情况判断
的正负情况判断![]() 的单调性。
的单调性。
(2)把f(x)≥﹣![]() +ax+b恒成立转化成b≤﹣alnx+x恒成立,令g(x)=﹣alnx+x,求出g′(x)=
+ax+b恒成立转化成b≤﹣alnx+x恒成立,令g(x)=﹣alnx+x,求出g′(x)=![]() ,判断g(x)的单调性,从而求得g(x)min=﹣alna+a,令h(a)=﹣alna+a,求得h′(a)=﹣lna>0,即可求得h(a)min,问题得解。
,判断g(x)的单调性,从而求得g(x)min=﹣alna+a,令h(a)=﹣alna+a,求得h′(a)=﹣lna>0,即可求得h(a)min,问题得解。
(1)∵f(x)=﹣alnx+(a+1)x﹣![]() (a>0),定义域为(0,+∞),
(a>0),定义域为(0,+∞),
∴![]() ,x>0
,x>0
令f′(x)=0,则x1=a,x2=1
①当0<a<1时,令f′(x)>0,则a<x<1;
令f′(x)<0,则0<x<a,或x>1,
∴f(x)在(0,a),(1,+∞)上单调递减;在(a,1)上单调递增;
②当a=1时,f′(x)≤0,且仅在x=1时,f′(x)=0,
∴f(x)在(0,+∞)单调递减;
③当a>1时,令f′(x)>0,则1<x<a;
令f′(x)<0,则0<x<1,或x>a,
∴在(0,1 ),(a,+∞)上单调递减;在(1,a)上单调递增.
综上所述,
当0<a<1时,f(x)在(0,a),(1,+∞)上单调递减;在(a,1)上单调递增;
当a=1时,f(x)在(0,+∞)上单调递减;
当a>1时,f(x)在(0,1),(a,+∞)上单调递减;在(1,a)上单调递增.
(2)∵f(x)=﹣alnx+(a+1)x﹣![]() (a>0)
(a>0)
若![]() 恒成立,
恒成立,
∴b≤﹣alnx+x恒成立
令g(x)=﹣alnx+x,x>0,
即b≤g(x)min,
∵g′(x)=![]() ,(a>0),
,(a>0),
∴g(x) 在(0,a)单调递减,(a,+∞) 单调递增;
g(x)min=g(a)=﹣alna+a
∴b≤﹣alna+a,a∈[![]() ,1],
,1],
令h(a)=﹣alna+a
∴h′(a)=﹣lna>0,∴h(a)单调递增,
∴h(a)min=h(![]() )=
)=![]() (1+ln2),
(1+ln2),
∴![]()
即b的最大值为![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】某地通过市场调查得到西红柿种植成本![]() (单位:元/千克)与上市时间
(单位:元/千克)与上市时间![]() (单位:
(单位:![]() 天)的数据如下表:
天)的数据如下表:
时间 |
|
|
|
种植成本 |
|
|
|
(1)根据上表数据,发现二次函数能够比较准确描述![]() 与
与![]() 的变化关系,请求出函数的解析式;
的变化关系,请求出函数的解析式;
(2)利用选取的函数,求西红柿最低种植成本及此时的上市天数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
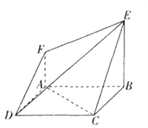
【题目】如图,在空间几何体ABCDFE中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() ,
,![]() .
.
(1)求证:AC//平面DEF;
(2)已知![]() ,若在平面
,若在平面![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(20)班共50名学生,在期中考试中,每位同学的数学考试分数都在区间![]() 内,将该班所有同学的考试分数分为七个组:
内,将该班所有同学的考试分数分为七个组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制出频率分布直方图如图所示.
,绘制出频率分布直方图如图所示.

(1)根据频率分布直方图,估计这次考试学生成绩的中位数和平均数;
(2)已知成绩为104分或105分的同学共有3人,现从成绩在![]() 中的同学中任选2人,则至少有1人成绩不低于106分的概率为多少?(每位同学的成绩都为整数)
中的同学中任选2人,则至少有1人成绩不低于106分的概率为多少?(每位同学的成绩都为整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com