
【题目】高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉(如图),并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.

(Ⅰ)理论上,小球落入4号容器的概率是多少?
(Ⅱ)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系中,点![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,以极点为原点,极轴为
的中点,以极点为原点,极轴为![]() 轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线
轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数 .
.
(1)求实数![]() 的值,并画出函数
的值,并画出函数![]() 的图象;
的图象;
(2)若函数![]() 在区间
在区间![]() 上是增函数,结合函数
上是增函数,结合函数![]() 的图象,求实数
的图象,求实数![]() 的取值范围;
的取值范围;
(3)结合图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三理科班共有60名同学参加某次考试,从中随机挑选出5名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 | 145 | 130 | 120 | 105 | 100 |
物理成绩 | 110 | 90 | 102 | 78 | 70 |
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(I)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(II)该班一名同学的数学成绩为110分,利用(I)中的回归方程,估计该同学的物理成绩;
(III)本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀. 若
该班数学优秀率与物理优秀率分别为50%和60%,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人,在答卷页上填写下面2×2列联表,判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关?
物理优秀 | 物理不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 | 60 |
参考数据:回归直线的系数
![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数有_________
(1)已知变量![]() 和
和![]() 满足关系
满足关系![]() ,则
,则![]() 与
与![]() 正相关;(2)线性回归直线必过点
正相关;(2)线性回归直线必过点![]() ;
;
(3)对于分类变量![]() 与
与![]() 的随机变量
的随机变量![]() ,
,![]() 越大说明“
越大说明“![]() 与
与![]() 有关系”的可信度越大
有关系”的可信度越大
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
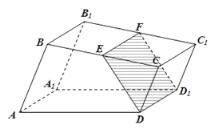
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com