
【题目】函数![]() 图象上不同两点
图象上不同两点![]() ,
,![]() 处切线的斜率分别是
处切线的斜率分别是![]() ,
,![]() 规定
规定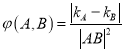 (
(![]() 为线段
为线段![]() 的长度)叫做曲线
的长度)叫做曲线![]() 在点
在点![]() 与
与![]() 之间的“平方弯曲度”,给出以下命题:
之间的“平方弯曲度”,给出以下命题:
①函数![]() 图象上两点
图象上两点![]() 与
与![]() 的横坐标分别为1和2,则
的横坐标分别为1和2,则![]() ;
;
②存在这样的函数,图象上任意两点之间的“平方弯曲度”为常数;
③设点![]() ,
,![]() 是抛物线
是抛物线![]() 上不同的两点,则
上不同的两点,则![]() ;
;
④设曲线![]() (
(![]() 是自然对数的底数)上不同两点
是自然对数的底数)上不同两点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最大值为
的最大值为![]() .
.
其中真命题的序号为__________(将所有真命题的序号都填上)
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,M是SB的中点,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.
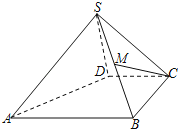
(1)证明:CD⊥SD;
(2)证明:CM∥面SAD;
(3)求四棱锥S﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包店随机收集了面包种类的有关数据,经分类整理得到下表:
面包类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
面包个数 | 90 | 60 | 30 | 80 | 100 | 40 |
好评率 | 0.6 | 0.45 | 0.7 | 0.35 | 0.6 | 0.5 |
好评率是指:一类面包中获得好评的个数与该类面包的个数的比值.
(1)从面包店收集的面包中随机选取1个,求这个面包是获得好评的第五类面包的概率;
(2)从面包店收集的面包中随机选取1个,估计这个面包没有获得好评的概率;
(3)面包店为增加利润,拟改变生产策略,这将导致不同类型面包的好评率发生变化.假设表格中只有两类面包的好评率数据发生变化,那么哪类面包的好评率增加0.1,哪类面包的好评率减少0.1,使得获得好评的面包总数与样本中的面包总数的比值达到最大?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,圆心
,圆心![]() 在
在![]() 轴上.
轴上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() (a>1).
(a>1).
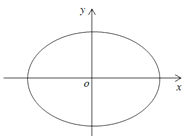
(Ⅰ)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(Ⅱ)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如图频率分布直方图:
五组,并作出如图频率分布直方图:
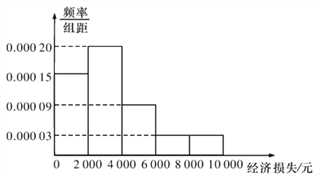
(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过4000元的居民中随机抽取2户进行捐款援助,设抽出损失超过8000元的居民为![]() 户,求
户,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如图,根据图表格中所给数据,分别求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并说明是否有
的值,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 |
|
| |
捐款不超过500元 |
|
| |
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到定点
到定点![]() 的距离之比它到直线
的距离之比它到直线![]() 的距离小1,设动点
的距离小1,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两个不同的点,过点
两个不同的点,过点![]() 分别作曲线
分别作曲线![]() 的切线,且二者相交于点
的切线,且二者相交于点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求证:![]() ;
;
(3)求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com