
【题目】上海市旅游节刚落下帷幕,在旅游节期间,甲、乙、丙三位市民顾客分别获得一些景区门票的折扣消费券,数量如表1,已知这些景区原价和折扣价如表2(单位:元).
表1:
数量 | 景区1 | 景区2 | 景区3 |
甲 | 0 | 2 | 2 |
乙 | 3 | 0 | 1 |
丙 | 4 | 1 | 0 |
表2:
门票 | 景区1 | 景区2 | 景区3 |
原价 | 60 | 90 | 120 |
折扣后价 | 40 | 60 | 80 |
(1)按照上述表格的行列次序分别写出这三位市民获得的折扣消费券数量矩阵A和三个景区的门票折扣后价格矩阵B;
(2)利用你所学的矩阵知识,计算三位市民各获得多少元折扣?
科目:高中数学 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( ).
①“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题;
中至少有一个不小于2”的逆命题是真命题;
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题;
”是一个真命题;
③命题![]() ,
,![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
④命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”.
”.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC-A1B1C1中,底面ABC是边长为2的等边三角形,上、下底面的面积之比为1:4,侧面A1ABB1⊥底面ABC,并且A1A=A1B1,∠AA1B=90°.
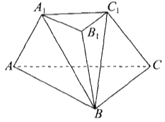
(1)平面A1C1B∩平面ABC=l,证明:A1C1∥l;
(2)求四棱锥B-A1ACC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了![]() 三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列
三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,试根据下列条件求出三款软件的激活码
,以此类推,试根据下列条件求出三款软件的激活码
(1)A款应用软件的激活码是该数列中第四个三位数的项数的平方
(2)B款应用软件的激活码是该数列中第一个四位数及其前所有项的和
(3)C款应用软件的激活码是满足如下条件的最小整数![]() :①
:①![]() ;②该数列的前
;②该数列的前![]() 项和为2的整数幂
项和为2的整数幂
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)求四边形![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,判断点
,判断点![]() 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
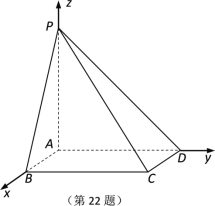
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com