
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
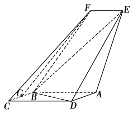
(1)求证:FG![]() 平面BED;
平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的![]() 点处,乙船在中间
点处,乙船在中间![]() 点处,丙船在最后面的
点处,丙船在最后面的![]() 点处,且
点处,且![]() .一架无人机在空中的
.一架无人机在空中的![]() 点处对它们进行数据测量,在同一时刻测得
点处对它们进行数据测量,在同一时刻测得![]() ,
, ![]() .(船只与无人机的大小及其它因素忽略不计)
.(船只与无人机的大小及其它因素忽略不计)

(1)求此时无人机到甲、丙两船的距离之比;
(2)若此时甲、乙两船相距100米,求无人机到丙船的距离.(精确到1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是直线
是直线![]() 上任意一点,过
上任意一点,过![]() 作
作![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 对应的方程;
对应的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 两点,(
两点,( ![]() 点在
点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求
,求![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
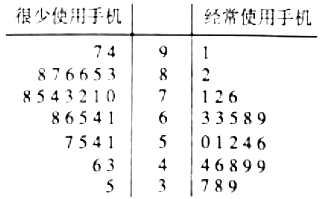
(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据: 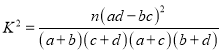 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地产数据研究所的数据显示,2016年该市新建住宅销售均价走势如下图所示,3月至7月房价上涨过快,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
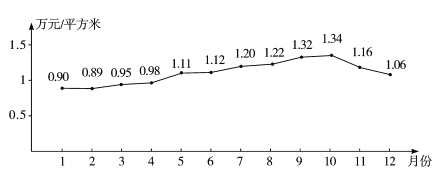
(1)地产数据研究所发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试求
之间具有较强的线性相关关系,试求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)政府若不调控,依次相关关系预测第12月份该市新建住宅的销售均价.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公示分别为:
中斜率和截距的最小二乘法估计公示分别为:
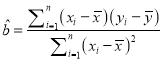 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 共焦点
共焦点![]() ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于![]() ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足![]() .
.
(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点![]() 作抛物线的切线
作抛物线的切线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,设线段AB的中点为
两点,设线段AB的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数;又定义行列式![]() =a1a4﹣a2a3; 函数g(θ)=
=a1a4﹣a2a3; 函数g(θ)=![]() (其中0≤θ≤
(其中0≤θ≤![]() ).
).
(1)证明:函数f(x)在(0,+∞)上也是增函数;
(2)若函数g(θ)的最大值为4,求m的值;
(3)若记集合M={m|任意的0≤θ≤![]() , g(θ)>0},N={m|任意的0≤θ≤
, g(θ)>0},N={m|任意的0≤θ≤![]() , f[g(θ)]<0},求M∩N.
, f[g(θ)]<0},求M∩N.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若f(1)= ![]() ,试求f(x)在区间[﹣2,6]上的最值.
,试求f(x)在区间[﹣2,6]上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com