【题目】已知二次函数的图象如图所示．
（1）写出该函数的零点；
（2）写出该函数的解析式．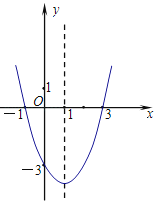
【答案】解：（1）由图象可知抛物线的与x轴的交点坐标是（﹣1，0），（3，0），
即当x=﹣1或3时，y=0
故该函数函数的零点是﹣1，3；
（2）设二次函数的解析式为y=a（x+1）（x﹣3）（a≠0），
将点（0，﹣3）代入代入解析式得：a（0+1）（0﹣3）=﹣3
解之得：a=1（6分）
∴函数的解析式是y=x2﹣2x﹣3．
【解析】（1）由图象可知抛物线的与x轴的交点坐标是（﹣1，0），（3，0），再结合零点的定义写出该函数的零点即可；
（2）由（1）可设抛物线解析式的交点式y=a（x+1）（x﹣3）（a≠0），再将点（0，﹣3）代入求a即可．
【考点精析】本题主要考查了二次函数的图象的相关知识点，需要掌握二次函数
的图象是一条抛物线，对称轴方程为
顶点坐标是
才能正确解答此题．
轻巧夺冠周测月考直通中考系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|lgx|﹣（ 
）x有两个零点x1 ， x2 ， 则有（ ）
A.x1x2＜0
B.x1x2=1
C.x1x2＞1
D.0＜x1x2＜1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数y=f（x）的图象如图所示．观察图象可知函数y=f（x）的定义域、值域分别是（ ）
A.[﹣5，0]∪[2，6），[0，5]
B.[﹣5，6），[0，+∞）
C.[﹣5，0]∪[2，6），[0，+∞）
D.[﹣5，+∞），[2，5]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知复数Z1 ， Z2在复平面内对应的点分别为A（﹣2，1），B（a，3）．
（1）若|Z1﹣Z2|= 
，求a的值．
（2）复数z=Z1Z2对应的点在二、四象限的角平分线上，求a的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数
、
、
，如果存在实数
使得
，那么称
为
、
的生成函数．
(1) 下面给出两组函数， 
是否分别为
、
的生成函数？并说明理由；
第一组： 
， 
， 
第二组： 
， 
， 
；
(2) 设
， 
， 
，生成函数
．若不等式
在
上有解，求实数
的取值范围；
(3) 设
， 
，取
，生成函数
图像的最低点坐标为
．若对于任意正实数
，且
，试问是否存在最大的常数
，使
恒成立？如果存在，求出这个
的值；如果不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束.除第五局甲队获胜的概率是
外，其余每局比赛甲队获胜的概率都是
.假设各局比赛结果相互独立.
（1）分别求甲队以3：0，3：1，3：2获胜的概率；
（2）若比赛结果为3：0或3：1，则胜利方得3分、对方得0分；若比赛结果为3:2，则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）设抛物线的顶点在坐标原点，焦点
在
轴正半轴上，过点的直线交抛物线于
两点，线段
的长是
，的中点到
轴的距离是
．
(1)求抛物线的标准方程；
(2)在抛物线上是否存在不与原点重合的点
，使得过点的直线交抛物线于另一点
，满足
，且直线
与抛物线在点处的切线垂直？并请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
