
| A. | 4+$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 设椭圆的左焦点为F',连接PF'、AF',根据椭圆的定义得|PA|+|PF|=4+(|PA|-|PF'|),结合图形可得当P、A、F'三点共线,且P在F'A延长线上时,|PA|-|PF'|取得最小值,利用两点之间距离公式,则不难求出这个最小值.
解答 解: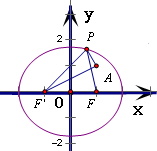 设椭圆的左焦点为F',连接PF'、AF'
设椭圆的左焦点为F',连接PF'、AF'
∵点P在椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上运动,
∴|PF|+|PF'|=2a=4
由此可得|PA|+|PF|=|PA|+(4-|PF'|)=4+(|PA|-|PF'|)
当P、A、F'三点共线,且P在F'A延长线上时,|PA|-|PF'|取得最小值
∴|PA|-|PF'|的最小值为:-|AF'|=$\sqrt{(1+1)^{2}+(1-0)^{2}}$=-$\sqrt{5}$
由此可得|PA|+|PF|的最大值为4-$\sqrt{5}$
故选:B.
点评 本题给出椭圆内部一点A和椭圆上动点P,求距离之和的最小值,着重考查了椭圆的标准方程和简单几何性质等知识,属于中档题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6π | B. | $\sqrt{6}π$ | C. | $\frac{3}{2}π$ | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
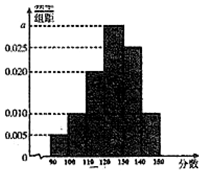 某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com