
| n2 | 3 |
| C | 2 35 |
| n2 |
| 3 |
| 28 |
| 35 |
| 4 |
| 5 |
| n2 |
| 3 |
| m2 |
| 3 |
| 7 | ||
|
| 1 |
| 85 |


科目:高中数学 来源: 题型:
| n2 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三9月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重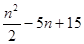 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为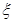 ,求E
,求E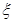 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
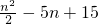 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省兰州一中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
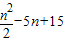 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com