
(本小题满分12分)
已知函数f(x)=x2+(2+lga)x+lgb,f(-1)=-2.
(1)求a与b的关系式;
(2)若f(x)≥2x恒成立,求a、b的值.
(1) a=10b;(2) a=100,b=10..
解析试题分析:(1)利用f(-1)=-2直接可得到lgb-lga=-1,从而得到a=10b.
(2)x2+xlga+lgb≥0对于任意x∈R恒成立,利用判别式及f(-1)=-2,即可求得a,b的值。
(1)∴lgb-lga=-1,即lgb=lga-1.a=10b
(2)又∵f(x)=x2+2x+xlga+lgb≥2x恒成立,∴x2+xlga+lgb≥0恒成立.
∴Δ=(lga)2-4lgb≤0.又lgb=lga-1,∴(lga-2)2≤0.∴lga-2=0.
∴lga=2,即a=100,b=10..
考点:函数恒成立问题,一元二次不等式的解法,函数的性质及其应用.
点评:本题的题型是函数恒成立问题,以此为载体主要考查不等式的解法,及学生分析解决问题的能力,因此我们必须提高解不等式的本领才能从容应对解决此类问题。


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动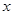 小时的收费为
小时的收费为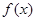 元
元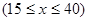 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动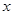 小时的收费为
小时的收费为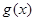 元
元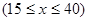 ,试求
,试求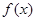 和
和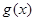 。
。
(2)问:小张选择哪家比较合算?说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)已知f(x)=m(x-2m)(x+m+3),g(x)=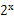 -2,若同时满足条件:
-2,若同时满足条件:
①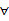 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②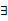 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元;当用水超过4吨时,超过部分每吨3.00元。某月甲、乙两户共交水费 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为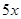 吨和
吨和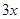 吨。
吨。
(1)求 关于
关于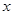 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com