
【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
③若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为
的最小值为![]()
④函数![]() 的最小值为
的最小值为![]()
正确的有__________.(把你认为正确的序号全部写上)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与直线
的直线与直线![]() 相交于点
相交于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率
的离心率![]() ;
;
(2)![]() 是圆
是圆![]() :
:![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
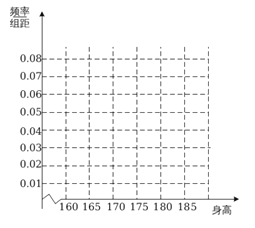
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,那么下列结论中错误的是( )
,那么下列结论中错误的是( )
A. 若![]() 是
是![]() 的极小值点,则
的极小值点,则![]() 在区间
在区间![]() 上单调递减
上单调递减
B. ![]() ,使
,使![]()
C. 函数![]() 的图像可以是中心对称图形
的图像可以是中心对称图形
D. 若![]() 是
是![]() 的极值点,则
的极值点,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为 ![]() .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为 ![]() .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ![]() ,求直线AP的方程.
,求直线AP的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1,
=1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.(12分)
)中恰有三点在椭圆C上.(12分)
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为﹣1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,且圆心在直线
,且圆心在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点,问在直线
两点,问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出点
恒成立?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com