
【题目】网络购物已经成为人们的一种生活方式.某购物平台为了给顾客提供更好的购物体验,为入驻商家设置了积分制度,每笔购物完成后,买家可以根据物流情况、商品质量等因素对商家做出评价,评价分为好评、中评和差评平台规定商家有50天的试营业时间,期间只评价不积分,正式营业后,每个好评给商家计1分,中评计0分,差评计![]() 分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
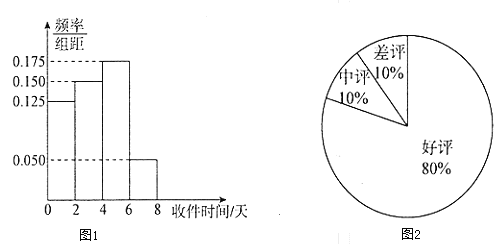
(1)通常收件时间不超过四天认为是物流迅速,否则认为是物流迟缓;
请根据题目所给信息完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“获得好评”与物流速度有关?
的把握认为“获得好评”与物流速度有关?
好评 | 中评或差评 | 合计 | |
物流迅速 | |||
物流迟缓 | 30 | ||
合计 |
(2)从正式营业开始,记商家在每笔交易中得到的评价得分为![]() .该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
.该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
表1
成交单数 | 36 | 30 | 27 |
天数 | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)平台规定,当积分超过10000分时,商家会获得“诚信商家”称号,请估计该商家从正式营业开始,1年内(365天)能否获得“诚信商家”称号
附: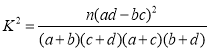
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)见解析,有![]() 的把握认为“获得好评”与物流速度有关.
的把握认为“获得好评”与物流速度有关.
(2)(Ⅰ)见解析,0.7(Ⅱ)该商家在1年内不能获得“诚信商家”称号.
【解析】
(1)先画出2×2列联表,再利用独立性检验求解;(2)(Ⅰ)先求出![]() 的取值可能是1,0,
的取值可能是1,0,![]() ,再求出对应的概率,写出其分布列,求出其期望得解;(Ⅱ)设商家每天的成交量为
,再求出对应的概率,写出其分布列,求出其期望得解;(Ⅱ)设商家每天的成交量为![]() ,求出商家每天能获得的平均积分和商家一年能获得的积分,即可判断得解.
,求出商家每天能获得的平均积分和商家一年能获得的积分,即可判断得解.
(1)由题意得
好评 | 中评或差评 | 合计 | |
物流迅速 | 50 | 5 | 55 |
物流迟缓 | 30 | 15 | 45 |
合计 | 80 | 20 | 100 |
![]() ,
,
所以有![]() 的把握认为“获得好评”与物流速度有关.
的把握认为“获得好评”与物流速度有关.
(2)(Ⅰ)由题意可知,![]() 的取值可能是1,0,
的取值可能是1,0,![]() ,
,
每位买家给商家作出好评、中评、差评的概率分别为0.8,0.1,0.1,
所以![]() 的分布列为
的分布列为
| 1 | 0 |
|
| 0.8 | 0.1 | 0.1 |
所以![]() ;
;
(Ⅱ)设商家每天的成交量为![]() ,则
,则![]() 的取值可能为27,30,36,
的取值可能为27,30,36,
所以![]() 的分布列为
的分布列为
| 27 | 30 | 36 |
| 0.4 | 0.4 | 0.2 |
所以![]() ,
,
所以商家每天能获得的平均积分为![]() ,
,
商家一年能获得的积分:![]() ,
,
所以该商家在1年内不能获得“诚信商家”称号.


科目:高中数学 来源: 题型:
【题目】在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(
变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(![]() 取近似值3.14)
取近似值3.14)
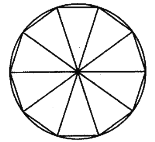
A.0.012B.0.052
C.0.125D.0.235
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:![]() )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
PM2.5 日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 |
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲乙两城市2020年5月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
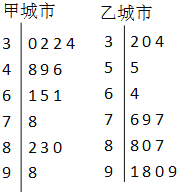
(1)根据你所学的统计知识估计甲乙两城市15天内哪个城市空气质量总体较好?并简要说明理由.
(2)在15天内任取1天,估计甲乙两城市空气质量类别均为优或良的概率;
(3)在乙城市15个监测数据中任取2个,设![]() 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
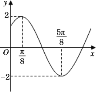
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,点A,B的坐标分别为![]() ,
,![]() ,P是坐标平面内的动点,且直线
,P是坐标平面内的动点,且直线![]() ,
,![]() 的斜率之积等于
的斜率之积等于![]() ,设点P的轨迹为C.
,设点P的轨迹为C.
(1)求轨迹C的方程;
(2)设过点![]() 且倾斜角不为0的直线
且倾斜角不为0的直线![]() 与轨迹C相交于M,N两点,求证:直线
与轨迹C相交于M,N两点,求证:直线![]() ,
,![]() 的交点在直线
的交点在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
,![]() )的部分图象如图所示,则下列结论正确的是( )
)的部分图象如图所示,则下列结论正确的是( )
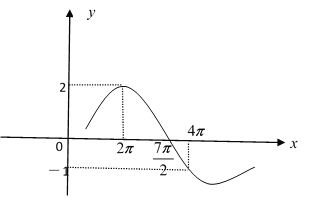
A.![]()
B.若把函数![]() 的图像向左平移
的图像向左平移![]() 个单位,则所得函数是奇函数
个单位,则所得函数是奇函数
C.若把![]() 的横坐标缩短为原来的
的横坐标缩短为原来的![]() 倍,纵坐标不变,得到的函数在
倍,纵坐标不变,得到的函数在![]() 上是增函数
上是增函数
D.![]() ,若
,若![]() 恒成立,则
恒成立,则![]() 的最小值为
的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“支付宝捐步”已经成为当下最热门的健身方式,为了了解是否使用支付宝捐步与年龄有关,研究人员随机抽取了5000名使用支付宝的人员进行调查,所得情况如下表所示:
50岁以上 | 50岁以下 | |
使用支付宝捐步 | 1000 | 1000 |
不使用支付宝捐步 | 2500 | 500 |
(1)由上表数据,能否有99.9%的把握认为是否使用支付宝捐步与年龄有关?
(2)55岁的老王在了解了捐步功能以后开启了自己的捐步计划,可知其在捐步的前5天,捐步的步数与天数呈线性相关.
第x天 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
步数 | 4000 | 4200 | 4300 | 5000 | 5500 |
(i)根据上表数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(ii)记由(i)中回归方程得到的预测步数为![]() ,若从5天中任取3天,记
,若从5天中任取3天,记![]() 的天数为X,求X的分布列以及数学期望.
的天数为X,求X的分布列以及数学期望.
附参考公式与数据: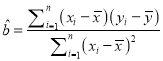 ,
,![]() ;K2=
;K2=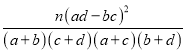 ;
;
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com