
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上为单调增函数.
在定义域上为单调增函数.
①求![]() 最大整数值;
最大整数值;
②证明: ![]() .
.
【答案】(1)![]() ;(2)①2;②见解析.
;(2)①2;②见解析.
【解析】试题分析:(1)根据导数几何意义得切线斜率为![]() ,再根据点斜式求切线方程(2)①先转化条件为
,再根据点斜式求切线方程(2)①先转化条件为![]() 恒成立,再根据
恒成立,再根据![]() ,得当
,得当![]() 时,
时, ![]() 恒成立.最后举反例说明当
恒成立.最后举反例说明当![]() 时,
时, ![]() 不恒成立.②对应要证不等式,在
不恒成立.②对应要证不等式,在![]() 中取
中取![]() ,得
,得![]() ,再根据等比数列求和公式得左边和为
,再根据等比数列求和公式得左边和为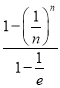 ,显然
,显然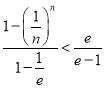 .
.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
则所求切线方程为![]() ,即
,即![]() .
.
(2)由题意知, ![]() ,
,
若函数![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则![]() 恒成立.
恒成立.
①先证明![]() .设
.设![]() ,则
,则![]() ,
,
则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() .
.
同理可证![]() ,∴
,∴![]() ,∴
,∴![]() .
.
当![]() 时,
时, ![]() 恒成立.
恒成立.
当![]() 时,
时, ![]() ,即
,即![]() 不恒成立.
不恒成立.
综上所述, ![]() 的最大整数值为2.
的最大整数值为2.
②由①知, ![]() ,令
,令![]() ,
,
∴![]() ,∴
,∴![]() .
.
由此可知,当![]() 时,
时, ![]() .当
.当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() .
.
累加得![]() .
.
又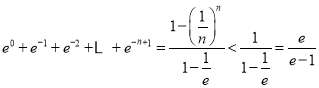 ,
,
∴![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】(2015·北京)某校老年、中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体状况,在抽取的样本
中,青年教师有320人,则该样本的老年教师人数为( )
A.90
B.100
C.180
D.300
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=1时,解不等式f(x)<0;
(2)若a>0,不等式f(x)<log2(x+ ![]() )恒成立,求a的取值范围;
)恒成立,求a的取值范围;
(3)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为 ![]() .
.
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为 ![]() 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 同时满足以下条件:①
同时满足以下条件:①![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;②
上是增函数;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)取函数![]() 的解析式;
的解析式;
(2)设![]() ,若存在实数
,若存在实数![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a,b,c分别为角A,B,C所对的边,且 ![]() a=2csinA.
a=2csinA.
(1)确定角C的大小;
(2)若c=3,且△ABC的面积为 ![]() ,求a2+b2的值.
,求a2+b2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果 ![]() 是二次函数,
是二次函数, ![]() 的图象开口向上,顶点坐标为(1,
的图象开口向上,顶点坐标为(1, ![]() )
) ![]() ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com