
【题目】如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证: 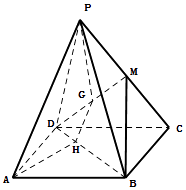
(1)AP∥平面BDM;
(2)AP∥GH.
【答案】
(1)证明:如图连AC,交BD于O,连接OM,
因为四边形ABCD是平行四边形,
所以O是AC的中点.
又M是PC的中点,
所以OM∥AP
又OM平面BDM,AP平面BDM,
所以AP∥平面BDM
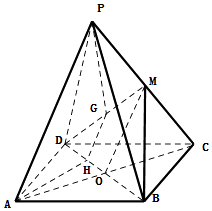
(2)证明:因为经过AP与点G的平面交平面BDM于GH,
所以由线面平行的性质定理得AP∥GH
【解析】(1)连AC,交BD于O,连接OM,证明OM∥AP,即可证明AP∥平面BDM;(2)由线面平行的性质定理得AP∥GH.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面平行的性质的理解,了解一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() =(2sinx,cosx+sinx),
=(2sinx,cosx+sinx), ![]() =(cosx,cosx﹣sinx),f(x)=
=(cosx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)﹣m=0(m∈R)在区间(0, ![]() )内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
)内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),直线l与y轴的交点为P.
(t为参数),直线l与y轴的交点为P.
(1)写出点P的极坐标(ρ,θ)(其中ρ>0,0≤θ<2π);
(2)求曲线 ![]() 上的点到P点距离的最大值.
上的点到P点距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线
中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线 ![]() (t为参数),曲线
(t为参数),曲线 ![]() ;
;
(1)将曲线 ![]() 化成普通方程,将曲线
化成普通方程,将曲线 ![]() 化成参数方程;
化成参数方程;
(2)判断曲线 ![]() 和曲线
和曲线 ![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称集合是“好集合”.给出下列4个集合:①
成立,则称集合是“好集合”.给出下列4个集合:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“好集合”的序号是( )
.其中为“好集合”的序号是( )
A. ①②④ B. ②③ C. ③④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+cosx,x∈R.
(1)求函数f(x)的最小正周期和最大值;
(2)函数y=f(x)的图象可由y=sinx的图象经过怎么的变换得到?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c在x=﹣1与x=2处都取得极值. (Ⅰ)求a,b的值及函数f(x)的单调区间;
(Ⅱ)若对x∈[﹣2,3],不等式f(x)+ ![]() c<c2恒成立,求c的取值范围.
c<c2恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com