
【题目】某中学为了了解全校学生的阅读情况,在全校采用随机抽样的方法抽取了60名学生(其中初中组和高中组各30名)进行问卷调查,并将他们在一个月内去图书馆的次数进行了统计,将每组学生去图书馆的次数分为5组: ![]() ,分别制作了如图所示的频率分布表和频率分布直方图.
,分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
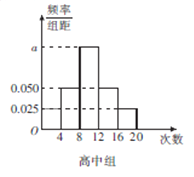
(1)完成频率分布表,并求出频率分布直方图中![]() 的值;
的值;
(2)在抽取的60名学生中,从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人,并用![]() 表示抽得的高中组的人数,求
表示抽得的高中组的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
使用时间 |
|
|
|
|
|
人数 | 10 | 40 | 25 | 20 | 5 |

(Ⅰ)已知该校大一学生由2400人,求抽取的100名学生中大一学生人数;
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为实数,
为实数,![]() ,
,![]() )
)
(1)若函数![]() 的图象过点
的图象过点![]() ,且方程
,且方程![]() 有且只有一个实根,求
有且只有一个实根,求![]() 的表达式;
的表达式;
(2)在(1)的条件下,当![]() 时,
时,![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=max{x2﹣ax+a,ax﹣a+1},其中max{x,y}= ![]() . (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
. (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
(Ⅱ)若a>1,求f(x)的最小值m(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题: ①若函数y=2x的定义域是{x|x≤0},则它的值域是{y|y≤1};
②若函数y= ![]() 的定义域是{x|x>2},则它的值域是{y|y≤
的定义域是{x|x>2},则它的值域是{y|y≤ ![]() };
};
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|﹣2≤x≤2};
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|0<x≤8}.
其中不正确的命题的序号是 . (注:把你认为不正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,过
,过![]() 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体![]() ,且这个几何体的体积为
,且这个几何体的体积为![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的长;
的长;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与
与![]() 垂直,如果存在,求线段
垂直,如果存在,求线段![]() 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com