
【题目】如图正方体ABCD﹣A1B1C1D1 , M,N分别为A1D1和AA1的中点,则下列说法中正确的个数为( ) 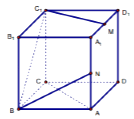
①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④B1A1、C1M、BN三条直线交于一点.
A.1
B.2
C.3
D.4
【答案】C
【解析】解:∵正方体ABCD﹣A1B1C1D1,M,N分别为A1D1和AA1的中点,
∴A1C1∥AC,C1M与A1C1相交,故①错误;
BD⊥AC,DD1⊥AC,故AC⊥平面BDD1,故BD1⊥AC,故②正确;、
连接BA1,则△A1BC1为等边三角形,即BC1与A1C1的所成角为60°;
由①中A1C1∥AC,可得BC1与AC的所成角为60°,故③正确;
④由MN∥AD1∥BC1,可得C1M、BN共面,
则C1M、BN必交于一点,
且该交点,必在B1A1上,
故B1A1、C1M、BN三条直线交于一点,故④正确;
故选:C
根据平行的定义,可判断①;先证明AC⊥平面BDD1,可判断②;根据△A1BC1为等边三角形,可判断③;根据公理3判断出三线共点,可判断④


科目:高中数学 来源: 题型:
【题目】直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC.设AB=2. 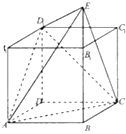
(1)求二面角E﹣AC﹣D1的大小;
(2)在D1E上是否存在一点P,使A1P∥面EAC?若存在,求D1P:PE的值;不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为 ![]() ,BC=
,BC= ![]() ,AC=1,∠ACB=90°,则此球的体积等于( )
,AC=1,∠ACB=90°,则此球的体积等于( )
A.![]() π
π
B.![]() π
π
C.![]() π
π
D.8π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是( )
A.若p或q为假命题,则p、q均为假命题.
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件.
C.命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
D.对于命题p:存在x∈R使得x2+x+1<0,则非p:存在x∈R,使x2+x+1≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求f(f( ![]() ));
));
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶不动点,求函数f(x)的二阶不动点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() , (Ⅰ)求函数f(x)的单调区间,并判断是否有极值;
, (Ⅰ)求函数f(x)的单调区间,并判断是否有极值;
(Ⅱ)若对任意的x>1,恒有ln(x﹣1)+k+1≤kx成立,求k的取值范围;
(Ⅲ)证明: ![]() (n∈N+ , n≥2).
(n∈N+ , n≥2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节是旅游消费旺季,某大型商场通过对春节前后20天的调查,得到部分日经济收入Q与这20天中的第x天(x∈N+)的部分数据如表:
天数x(天) | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
日经济收入Q(万元) | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
(1)根据表中数据,结合函数图象的性质,从下列函数模型中选取一个最恰当的函数模型描述Q与x的变化关系,只需说明理由,不用证明. ①Q=ax+b,②Q=﹣x2+ax+b,③Q=ax+b,④Q=b+logax.
(2)结合表中的数据,根据你选择的函数模型,求出该函数的解析式,并确定日经济收入最高的是第几天;并求出这个最高值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C的对边分别是a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B.
(2)若 ![]() ,△ABC的周长为
,△ABC的周长为 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点. 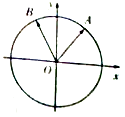
(I)若A,B两点的纵会标分别为 ![]() 的值;
的值;
(II)已知点C是单位圆上的一点,且 ![]() 的夹角θ.
的夹角θ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com