
| A. | (1,2) | B. | (1,$\sqrt{2}$) | C. | ($\sqrt{2}$,2) | D. | (2,+∞) |
分析 根据题意,求出AF,$\frac{1}{2}$|BC若△ABC为锐角三角形,只要∠FAB为锐角,即$\frac{1}{2}$|BC|<AF;从而可得结论.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,左焦点为F,AF=a+c,$\frac{1}{2}$|BC|=$\frac{{b}^{2}}{a}$
过F作垂直于x轴的直线与双曲线相交于B、C两点,若△ABC为锐角三角形,
只要∠FAB为锐角,即$\frac{1}{2}$|BC|<AF;
所以有 $\frac{{b}^{2}}{a}$<a+c,
即c2-a2<a2+ac,即:e2-e-2<0
解出e∈(1,2),
故选:A.
点评 本题考查双曲线的离心率和锐角三角形的判断,在解题过程中要注意隐含条件的挖掘.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$π | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}π$ | D. | $\frac{4}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
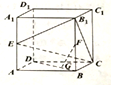 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (0,e) | C. | (e,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com