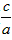Question

已知函数f（x）=ax²+bx+c中，a+b+c=0，a>b>c。
（Ⅰ）证明函数f（x）有两个不同的零点；
（Ⅱ）若存在x∈R，使ax²+bx+a+c=0成立。
①试判断f（x+3）的符号，并说明理由；
②当b≠0时，证明关于x的方程ax²+bx+a+c=0在区间（，0）和（0，1）内各有一个实根。

Answer 1

解：因为a+b+c=0，a>b>c，
所以b=-a-c，a>0，c＜0；
（Ⅰ）证明：因为二次方程f（x）=0的根的判别式，
△=b²-4ac=（-a-c）²-4ac=（a-c）²，
由a>c，得△=（a-c）²>0，
故方程f（x）=0有两个不同的实根，即函数f（x）有两个不同的零点；
（Ⅱ）由ax²+bx+a+c=0，得f（x）=-a，
①函数f（x）的图象为开口向上的抛物线，
由f（x）=-a＜0，知实数x介于方程f（x）=0的 两根之间，
由于f（1）=a+b+c=0，则1是方程f（x）=0的一个根，
又由根与系数的关系，得另一个根为，
由a+b+c=0，a>b，得a>-a-c
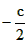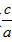所以a>，即>-2
故x+3>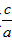+3>-2+3=1
因此f（x+3）为正，
②令g（x）=ax²+bx+a+c，则g（x）=f（x）+a，
所以，g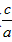（）=f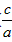（）+a=a>0，
g（1）=f（1）+a>0
因为二次方程ax²+bx+a+c=0有实数根，所以
△=b²-4a（a+c）=（-a-c）²-4a（a+c）
=-3a²-2ac+c²≥0，
即（3a-c）（a+c）≤0，
解得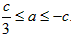
又a>0，且b=-（a+c）≠0，
所以0＜a＜-c，
所以a+c＜0，
故g（0）=f（0）+a=a+c＜0，
因此，关于x的方程ax²+bx+a+c=0在区间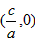和（0，1）内各有一个实根。