
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() ∶
∶![]() 和圆
和圆![]() ∶
∶![]() ,
,![]() 是直线
是直线![]() 上一点,过点
上一点,过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)若![]() ,求点
,求点![]() 坐标;
坐标;
(2)若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)设线段![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出![]() 到圆心的距离为
到圆心的距离为![]() ,设
,设![]() ,解方程
,解方程![]() 即得解;(2)设
即得解;(2)设![]() ,若圆
,若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,分析得到
,分析得到![]() ,即
,即![]() ,解不等式得解;(3)设
,解不等式得解;(3)设![]() ,可得
,可得![]() 所在直线方程:
所在直线方程:![]() ,
,![]() 点的轨迹为:
点的轨迹为: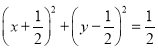 ,根据
,根据![]() 求出最大值得解.
求出最大值得解.
(1)若![]() ,则四边形
,则四边形![]() 为正方形,
为正方形,
则![]() 到圆心的距离为
到圆心的距离为![]() ,
,
∵![]() 在直线
在直线![]() 上,设
上,设![]()
故![]() ,解得
,解得![]() ,故
,故![]() ;
;

(2)设![]() ,若圆
,若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
过![]() 作圆的切线
作圆的切线![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在直角三角形![]() 中,∵
中,∵![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 横坐标的取值范围为:
横坐标的取值范围为:![]() ;
;
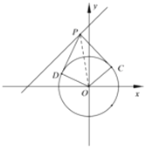
(3)设![]() ,则以
,则以![]() 为直径的圆的方程为
为直径的圆的方程为
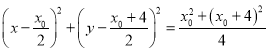
化简得![]() ,与
,与![]() 联立,
联立,
可得![]() 所在直线方程:
所在直线方程:![]() ,
,
联立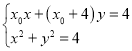 ,得
,得![]() ,
,
∴![]() 的坐标为
的坐标为 ,
,
可得![]() 点的轨迹为:
点的轨迹为: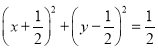 ,
,
圆心![]() ,半径
,半径![]() .其中原点
.其中原点![]() 为极限点(也可以去掉).
为极限点(也可以去掉).
由题意可知![]() ,∴
,∴ .
.
∴![]() .
.
∴线段![]() 的最大值为
的最大值为![]() .
.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,平面
为菱形,平面![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
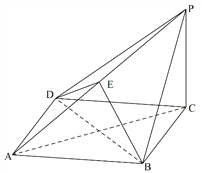
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的
的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x+1)2+(y-3)2=9和圆C2:x2+y2-4x+2y-11=0.
(1)求两圆公共弦所在直线的方程;
(2)求直线过点C(3,-5),且与公共弦垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2ex﹣b,其中b∈R.
(Ⅰ)证明:对于任意x1,x2∈(﹣∞,0],都有f(x1)﹣f(x2)![]() ;
;
(Ⅱ)讨论函数f(x)的零点个数(结论不需要证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(CCTV-1)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 两个地区的
两个地区的![]() 名观众,得到如下的
名观众,得到如下的![]() 列联表:
列联表:
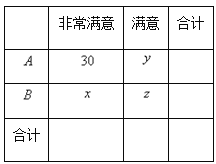
已知在被调查的![]() 名观众中随机抽取
名观众中随机抽取![]() 名,该观众是
名,该观众是![]() 地区当中“非常满意”的观众的概率为
地区当中“非常满意”的观众的概率为![]() ,且
,且![]() .
.
(1)现从![]() 名观众中用分层抽样的方法抽取
名观众中用分层抽样的方法抽取![]() 名进行问卷调查,则应抽取“满意”的
名进行问卷调查,则应抽取“满意”的![]() 地区的人数各是多少.
地区的人数各是多少.
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)若以抽样调查的频率为概率,从![]() 地区随机抽取
地区随机抽取![]() 人,设抽到的观众“非常满意”的人数为
人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
|
|
|
|
|
|
|
|
附:参考公式:
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com