
【题目】(本小题满分12分)已知函数![]() (
(![]() )的最小正周
)的最小正周
期为![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将函数![]() 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]()
的图像,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(1)1;(2)1.
【解析】试题分析:(Ⅰ)将函数式整理变形为![]() 的形式,由函数周期可求得
的形式,由函数周期可求得![]() 的值;(Ⅱ)由(Ⅰ)中求得的函数式按照平移规律得到函数
的值;(Ⅱ)由(Ⅰ)中求得的函数式按照平移规律得到函数![]() ,由定义域求得
,由定义域求得![]() 的取值范围,结合函数单调性可求得函数的最小值
的取值范围,结合函数单调性可求得函数的最小值
试题解析:(Ⅰ)∵f(x)=sin(π﹣ωx)cosωx+cos2ωx,
∴f(x)=sinωxcosωx+![]()
=![]() sin2ωx+
sin2ωx+![]() cos2ωx+
cos2ωx+![]()
=![]() sin(2ωx+
sin(2ωx+![]() )+
)+![]()
由于ω>0,依题意得![]() ,
,
所以ω=1;
(Ⅱ)由(Ⅰ)知f(x)=![]() sin(2x+
sin(2x+![]() )+
)+![]() ,
,
∴g(x)=f(2x)=![]() sin(4x+
sin(4x+![]() )+
)+![]()
∵0≤x≤![]() 时,
时,![]() ≤4x+
≤4x+![]() ≤
≤![]() ,
,
∴![]() ≤sin(4x+
≤sin(4x+![]() )≤1,
)≤1,
∴1≤g(x)≤![]() ,
,
g(x)在此区间内的最小值为1.


科目:高中数学 来源: 题型:
【题目】
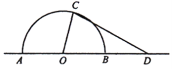
如图,某城市有一块半径为40![]() 的半圆形(以
的半圆形(以![]() 为圆心,
为圆心,![]() 为直径)绿化区域,现计划对其进行改建,在
为直径)绿化区域,现计划对其进行改建,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,在半圆上选定一点
,在半圆上选定一点![]() ,改建后的绿化区域由扇形区域
,改建后的绿化区域由扇形区域![]() 和三角形区域
和三角形区域![]() 组成,其面积为
组成,其面积为![]() ,设
,设![]()
(1)写出![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)试问![]() 多大时,改建后的绿化区域面积
多大时,改建后的绿化区域面积![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下![]() 组:第1组
组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求a的值;
(Ⅱ)现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生座谈,求每组抽取的学生人数;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计随机抽取学生所得测试分数的平均值在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式:  ,
, ![]() =
=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 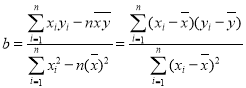 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为:
 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)2lnx,a∈R.
(I)若x=e是y=f(x)的极值点,求实数a的值;
(Ⅱ)若函数y=f(x)﹣4e2只有一个零点,求实数a的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com