Question

【题目】如果四面体的四条高交于一点，则该点称为四面体的垂心，该四面体称为垂心四面体.

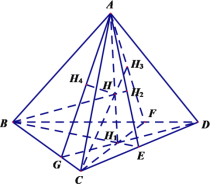
（1）证明：如果四面体的对棱互相垂直，则该四面体是垂心四面体；反之亦然.

（2）给出下列四面体

①正三棱锥；

②三条侧棱两两垂直；

③高在各面的射影过所在面的垂心；

④对棱的平方和相等.

其中是垂心四面体的序号为 .

Answer 1

【答案】（1）证明见解析（2）①②③④

【解析】

（1）首先证明四面体的两条高线交于一点，再证过另一顶点和这一点的直线为另一条高线，即可证明结论成立.（2）①②③可通过证明对棱垂直证明是垂心四面体，④假设四面体为垂心四面体，则可证明有对棱的平方和相等，逆推依然成立，所以④也成立.

（1）先证对棱互相垂直的四面体是垂心四面体.

作，则

，

此时两条高线

连接，下证

.连接

综上可知，四条高线交于点，故该四面体为垂心四面体；

反之，若该四面体为垂心四面体，即四条高线交于点.

,,，故,

同理可证

（2）①正三棱锥底面为正三角形，侧面为全等的等腰三角形，可证明三组对棱两两垂直，所以①符合要求.②三条侧棱两两垂直，任一条侧棱垂直另外两条侧棱所在的平面，也可证明对棱垂直，所以②符合要求.③高垂直于底面棱，在侧面的射影垂直于此面的底面棱，所以底面棱垂直于高和射影所在的平面，即垂直于对棱，所以③符合要求.④假设四面体为垂心四面体，设BF交CD于E，则AC2﹣AD2＝CF2﹣DF2＝CE2﹣DE2＝BC2﹣BD2，即AC2+BD2＝AD2+BC2，反之，若故AC2+BD2＝AD2+BC2，则有C2﹣AD2＝CF2﹣DF2＝CE2﹣DE2＝BC2﹣BD2成立，即同理可证其他，故④符合要求．

①②③④均符合要求.