
【题目】数列![]()
满足:![]() 或1(k=1,2,…,n-1).
或1(k=1,2,…,n-1).
对任意i,j,都存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
(I)若m=2,写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2; ②1,1,1,1,2,2,2,2; ③1,1,1,1,1,2,2,2,2
(II)记![]() .若m=3,求S的最小值;
.若m=3,求S的最小值;
(III)若m=2018,求n的最小值.
【答案】(Ⅰ)②③;(Ⅱ)见解析;(Ⅲ)2026.
【解析】分析:(Ⅰ)分别把所给的三个数列代入题目条件中进行验证后可得出结果.(Ⅱ)当m=3时,设数列An中1,2,3出现频数依次为![]() ,由题意
,由题意![]() .假设
.假设![]() ,则与已知矛盾,从而
,则与已知矛盾,从而![]() ,同理可证
,同理可证![]() .假设
.假设![]() ,则与已知矛盾,所以
,则与已知矛盾,所以![]() ,由此能证明
,由此能证明![]() .(Ⅲ)设1,2,…,2018出现频数依次为
.(Ⅲ)设1,2,…,2018出现频数依次为![]() ,可得
,可得![]() ,则
,则![]() .取
.取![]() ,
,![]() ,得到的数列为:
,得到的数列为:![]()
![]() ,由此能出n的最小值.
,由此能出n的最小值.
详解:(I)数列![]() 满足:
满足:![]() 或1(k=1,2,…,n-1).对任意i,j,都存在s,t,使得
或1(k=1,2,…,n-1).对任意i,j,都存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
∴在①中,1,1,1,2,2,2,不符合题目条件;
在②中,1,1,1,1,2,2,2,2,符合题目条件;
在③中,1,1,1,1,1,2,2,2,2,符合题目条件.
故所有符合题目条件的数列的序号为②③.
(II)当m=3时,设数列![]() 中1,2,3,出现频数依次为
中1,2,3,出现频数依次为![]() ,由题意
,由题意![]() .
.
①假设![]() ,则有
,则有![]() (对任意
(对任意![]() ),
),
与已知矛盾,所以![]() .
.
同理可证:![]() .
.
②假设![]() ,则存在唯一的
,则存在唯一的![]() ,使得
,使得![]() .
.
则对![]() ,有
,有![]() (k,s,t两两不相等),与已知矛盾,
(k,s,t两两不相等),与已知矛盾,
所以![]() .
.
综上![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
故S的最小值为20.
(III)设1,2,…,2018出现频数依次为![]() .
.
同(II)的证明,可得![]() ,
,
所以![]() .
.
取![]() ,
,![]() ,得到的数列为:
,得到的数列为:
![]()
下面证明![]() 满足题目要求.
满足题目要求.
对![]() ,不妨令
,不妨令![]() ,
,
①如果![]() 或
或![]() ,由于
,由于![]() ,所以符合条件;
,所以符合条件;
②如果![]() 或
或![]() ,
,
由于![]() ,
,![]() ,
,
所以也成立;
③如果![]() ,则可选取
,则可选取![]() ;同样的,如果
;同样的,如果![]() ,则可选取
,则可选取![]() ,使得
,使得![]() ,且i,j,s,t两两不相等;
,且i,j,s,t两两不相等;
④如果![]() ,则可选取
,则可选取![]() ,注意到这种情况每个数最多被选取了一次,因此也成立.
,注意到这种情况每个数最多被选取了一次,因此也成立.
综上对任意i,j,总存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
因此![]() 满足题目要求,
满足题目要求,
所以n的最小值为2026.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logax(a>1)在[a,2a]上的最大值是最小值的2倍.
(1)若函数g(x)=f(3x2-mx+5)在区间[-1,+∞)上是增函数,求实数m的取值范围;
(2)设函数F(x)=f(![]() )(2x),且关于x的方程F(x)=k在[
)(2x),且关于x的方程F(x)=k在[![]() ,4]上有解,求实数k的取值范围.
,4]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1﹣x﹣ax2 . (Ⅰ)当a=0时,求证:f(x)≥0;
(Ⅱ)当x≥0时,若不等式f(x)≥0恒成立,求实数a的取值范围;
(Ⅲ)若x>0,证明(ex﹣1)ln(x+1)>x2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象关于点(-1,0)对称,且当x∈(-∞,0)时,
的图象关于点(-1,0)对称,且当x∈(-∞,0)时,![]() 成立,(其中f′(x)是f(x)的导数);若
成立,(其中f′(x)是f(x)的导数);若![]() ,
, ![]() ,
,![]() ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A. a>b>c B. b>a>c C. c>a>b D. c>b>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知椭圆C1:![]() +
+![]() =1,C2:
=1,C2:![]() +
+![]() =1(a>b>0)有相同的离心率,F(﹣
=1(a>b>0)有相同的离心率,F(﹣![]() , 0)为椭圆C2的左焦点,过点F的直线l与C1、C2依次交于A、C、D、B四点.
, 0)为椭圆C2的左焦点,过点F的直线l与C1、C2依次交于A、C、D、B四点.
(1)求椭圆C2的方程;
(2)求证:无论直线l的倾斜角如何变化恒有|AC|=|DB|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的方程(x﹣1)4+mx﹣m﹣2=0各个实根x1 , x2…xk(k≤4,k∈N*)所对应的点(xi![]() ),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
A.(﹣1,7)
B.(﹣∞,﹣7)U(﹣1,+∞)
C.(﹣7,1)
D.(﹣∞,1)U(7,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化.某调查机构随机抽取8名购物者进行采访,4名男性购物者中有3名倾向于网购,1名倾向于选择实体店,4名女性购物者中有2名倾向于选择网购,2名倾向于选择实体店.
(1)若从8名购物者中随机抽取2名,其中男女各一名,求至少1名倾向于选择实体店的概率:
(2)若从这8名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:

已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为![]()
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.5%的把握认为喜欢打篮球与性别有关?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: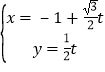 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com