
分析 (1)由S3=9.可求得a2=3,d=a2-a1=2,根据等差数列通项公式即可求得an,a5=b3,求得q2=9,数列{bn}的各项均为正数,即可求得q=3,根据等比数列通项公式即可求得bn;
(2)首先求得Sn+1=n2+n=n(n+1),$\frac{1}{{S}_{n}+n}$=$\frac{1}{n(n+1)}$,采用“裂项法“求得$\frac{1}{{S}_{n}+n}$=$\frac{1}{n}$-$\frac{1}{n+1}$,代入整理即可求得$\frac{1}{{S}_{1}+1}$+$\frac{1}{{S}_{2}+1}$+…+$\frac{1}{{S}_{n}+n}$的值.
解答 解:(1)设等差数列{an}的公差为d,等比数列的公比为q,
S3=a1+a2+a3=9.即a2=3,
d=a2-a1=2,
∴数列{an}的通项公式an=2n-1,
a5=b3=9,即q2=9,
∵bn>0,
∴q=3,
∴数列{bn}的通项公式bn=3n-1;
(2)由等差数列前n项和公式Sn=$\frac{n(1+2n-1)}{2}$=n2,
Sn+n=n2+n=n(n+1),
∴$\frac{1}{{S}_{n}+n}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
$\frac{1}{{S}_{1}+1}$+$\frac{1}{{S}_{2}+1}$+…+$\frac{1}{{S}_{n}+n}$=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$),
=1-$\frac{1}{n+1}$,
=$\frac{n}{n+1}$.
$\frac{1}{{S}_{1}+1}$+$\frac{1}{{S}_{2}+1}$+…+$\frac{1}{{S}_{n}+n}$=$\frac{n}{n+1}$.
点评 本题考查了等差数列与等比数列的通项公式、“裂项法”、等插数列的前n项和公式,考查了推理能力与计算能力,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为平行四边形,AB=1,AC=$\sqrt{3}$,AD=2,M、N分别为棱PA、BC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为平行四边形,AB=1,AC=$\sqrt{3}$,AD=2,M、N分别为棱PA、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
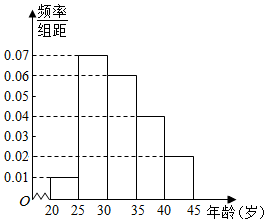 为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人
为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人查看答案和解析>>
科目:高中数学 来源: 题型:选择题
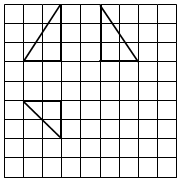 如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )
如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )| A. | 12π | B. | 34π | C. | $\frac{17π}{4}$ | D. | 17π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点
如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com