练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的参数方程为（为参数， ）.以原点为极点，以轴正半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系.设曲线的极坐标方程为.

    （Ⅰ）设为曲线上任意一点，求的取值范围；

    （Ⅱ）若直线与曲线交于两点， ，求的最小值.

    【答案】（1）（2）4.

    【解析】试题分析: (1)将曲线C的极坐标方程化为直角坐标方程,将化为关于 的二次函数,求出范围; (2)将直线的参数方程代入曲线C的直角坐标方程中,由直线参数方程的几何意义求出 表达式,求出最小值.

    试题解析:（1）将曲线的极坐标方程化为直角坐标方程为，

    ∵为曲线上任意一点，∴，

    ∴的取值范围是；

    （2）将代入，整理，得，

    ∴，设方程的两根分别为，

    所以，

    当时， 取得最小值4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，过上一点的切线的方程为.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设过点且斜率不为的直线交椭圆于两点，试问轴上是否存在点，使得？若存在，求出点的坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左顶点为A，右焦点为F，过点F的直线交椭圆于B，C两点．

    (1)求该椭圆的离心率；

    (2)设直线AB和AC分别与直线x＝4交于点M，N，问：x轴上是否存在定点P使得MP⊥NP？若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某机械厂今年进行了五次技能考核，其中甲、乙两名技术骨干得分的平均分相等，成绩统计情况如茎叶图所示（其中是09的某个整数）

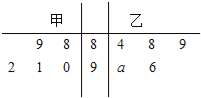
    （1）若该厂决定从甲乙两人中选派一人去参加技能培训，从成绩稳定性角度考虑，你认为谁去比较合适？

    （2）若从甲的成绩中任取两次成绩作进一步分析，在抽取的两次成绩中，求至少有一次成绩在（90，100]之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．　

    （Ⅰ）若，证明：函数是上的减函数；

    （Ⅱ）若曲线在点处的切线与直线平行，求的值；

    （Ⅲ）若，证明： （其中…是自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=x2+bx+c，若f（﹣3）=f（1），f（0）=﹣3．
    （1）求函数f（x）的解析式；
    （2）若函数g（x）= 画出函数g（x）图象；
    （3）求函数g（x）在[﹣3，1]的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆与双曲线有相同的焦点，，椭圆的一个短轴端点为，直线与双曲线的一条渐近线平行，若椭圆于双曲线的离心率分别为，，则的最小值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

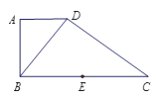
    【题目】如图，在直角梯形中， // ， ⊥， ⊥, 点是边的中点, 将△沿折起，使平面⊥平面，连接, , , 得到如

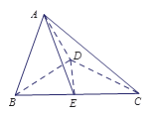
    图所示的空间几何体.

    （Ⅰ）求证： ⊥平面；

    （Ⅱ）若，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥的底面为平行四边形，且,, 分别为中点，过作平面分别与线段相交于点.

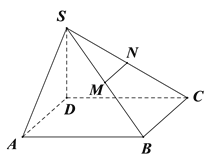
    （Ⅰ）在图中作出平面使面‖ (不要求证明）；

    （II）若，在（Ⅰ）的条件下求多面体的体积.

    查看答案和解析>>

    同步练习册答案