
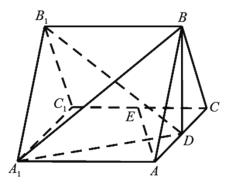
【题目】如图,直三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,求得
轴建立如图所示的空间直角坐标系,求得![]() ,证得
,证得![]() ,
,![]() ,即可求解;
,即可求解;
(2)由(1)得到![]() ,即为平面
,即为平面![]() 的一个法向量,结合向量的夹角公式,即可求解;
的一个法向量,结合向量的夹角公式,即可求解;
(3)求得平面![]() 的法向量
的法向量![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
由直三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() 是
是![]() 中点,
中点,![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
由![]() 分别为
分别为![]() 的中点,可得
的中点,可得![]() ,可得
,可得![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由(1)可得![]() 平面
平面![]() ,则
,则![]() ,即为平面
,即为平面![]() 的一个法向量,
的一个法向量,
又由![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
可得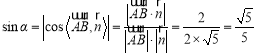 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)设平面![]() 的法向量
的法向量![]() ,
,
因为![]() ,可得
,可得 ,即
,即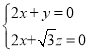 ,
,
不妨取![]() ,得
,得![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,
,
由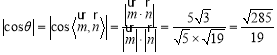 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为![]() ,客场取胜的概率为
,客场取胜的概率为![]() ,且各场比赛结果相互独立,则甲队不超过
,且各场比赛结果相互独立,则甲队不超过![]() 场即获胜的概率是( )
场即获胜的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将n×n的棋盘的部分结点(单位正方形的顶点)染红,使得任意一个由单位正方形构成的k×k![]() 的子棋盘的边界上至少有一个红点.记满足条件的红点数的最小值为
的子棋盘的边界上至少有一个红点.记满足条件的红点数的最小值为![]() . 试求
. 试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司为了方便市民出行、科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为研究车辆发车间隔时间![]() (分钟)与乘客等候人数
(分钟)与乘客等候人数![]() (人)之间的关系,经过调查得到如下数据:
(人)之间的关系,经过调查得到如下数据:
间隔时间 |
|
|
|
|
|
|
等候人数 |
|
|
|
|
|
|
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过
的差,若差值的绝对值不超过![]() ,则称所求线性回归方程是“恰当回归方程”.
,则称所求线性回归方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间之差大于
组数据的间隔时间之差大于![]() 的概率;
的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)在(2)的条件下,为了使等候的乘客不超过![]() 人,则间隔时间最多可以设置为多少分钟?(精确到整数)
人,则间隔时间最多可以设置为多少分钟?(精确到整数)
参考公式: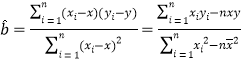 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的点A(4,t)到其焦点F的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F作直线l,使得抛物线C上恰有三个点到直线1的距离为2,求直线1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了改善市民的生活环境,信阳市决定对信阳市的1万家中小型化工企业进行污染情况摸排,并出台相应的整治措施.通过对这些企业的排污口水质,周边空气质量等的检验,把污染情况综合折算成标准分100分,发现信阳市的这些化工企业污染情况标准分基本服从正态分布N(50,162),分值越低,说明污染越严重;如果分值在[50,60]内,可以认为该企业治污水平基本达标.
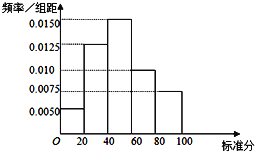
(1)如图是信阳市的某工业区所有被调查的化工企业的污染情况标准分的频率分布直方图,请计算这个工业区被调查的化工企业的污染情况标准分的平均值,并判断该工业区的化工企业的治污平均值水平是否基本达标;
(2)大量调査表明,如果污染企业继续生产,那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元,标准分在[18,34)内的化工企业每月对周边造成的直接损失约为4万元.长沙市决定关停80%的标准分低于18分的化工企业和60%的标准分在[18,34)内的化工企业,每月可减少的直接损失约有多少?
(附:若随机变量![]() ,则
,则![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com