
【题目】已知集合A={x||x﹣a|≤3,x∈R},B={x|x2﹣3x﹣4>0,x∈R}.
(1)若a=1,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
【答案】
(1)解:当a=1时,A={﹣2≤x≤4},
在集合B中,由x2﹣3x﹣4>0可得x<﹣1或x>4
所以A∩B={x|﹣2≤x<﹣1}
(2)解:集合A中,由|x﹣a|≤3可得﹣3≤x﹣a≤3,即a﹣3≤x≤a+3,
由A∪B=R可得,a﹣3≤﹣1且a+3≥4,
所以1≤a≤2
【解析】(1)当a=1时,A={﹣2≤x≤4},再求出集合B,由此能求出A∩B.(2)集合A中,a﹣3≤x≤a+3,由A∪B=R可得,a﹣3≤﹣1且a+3≥4,由此能求出实数a的范围.
【考点精析】掌握集合的并集运算和集合的交集运算是解答本题的根本,需要知道并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;交集的性质:(1)A∩B
B,反之也成立;交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]()
![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD.
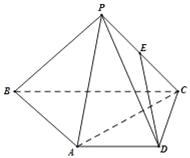
(1)证明:ED∥面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数 ![]() ,
,
(1)求函数f(x)的定义域;
(2)将函数y=f(x)的图象向右平移两个单位后得到函数y=g(x)的图象,若实数x满足g(x)≥0,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)讨论![]() 在区间
在区间![]() 上的极值点个数;
上的极值点个数;
(3)是否存在![]() ,使得
,使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切?若存在,求出所有
轴相切?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC= ![]() ,AB=1,BD=PA=2,M 为PD的中点.
,AB=1,BD=PA=2,M 为PD的中点. 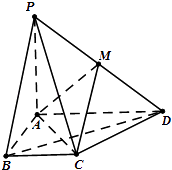
(1)求异面直线BD与PC所成角的余弦值;
(2)求二面角A﹣MC﹣D的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com