练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知二阶矩阵M属于特征值一1的一个特征向量为
    1
    -2
    ，属于特征值2的一个特征向量为
    1
    1
    ，求矩阵M及其逆矩阵M-1．
    分析：利用特征值与特征向量的定义，建立方程组，即可求得M，求出M的行列式，即可求得逆矩阵M-1．
    解答：解：设M=
    ab
    cd
    ，则由题意
    ab
    cd
    1
    -2
    =（-1）×
    1
    -2
    ，
    ab
    cd
    1
    1
    =2
    1
    1

    ∴
    a-2b=-1
    c-2d=2
    ，
    a+b=2
    c+d=2

    ∴a=b=1，c=2，d=0
    ∴M=
    11
    20

    ∵M的行列式
    .
    11
    20
    .
    =-2
    ∴逆矩阵M-1=
    0
    1
    2
    1-
    1
    2
    ．
    点评：本题主要考查了二阶矩阵，以及特征值与特征向量的计算，考查逆矩阵，正确理解特征值与特征向量是关键，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    [选做题]已知二阶矩阵M属于特征值3的一个特征向量为
    e
    =
    1
    1
    ，并且矩阵M对应的变换将点（-1，2）变成点（9，15），求出矩阵M．

    查看答案和解析>>

    科目：高中数学 来源：2012届江苏南京学大教育专修学校高三五月数学试卷（解析版） 题型：解答题

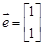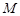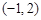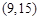    已知二阶矩阵M属于特征值3的一个特征向量为，并且矩阵对应的变换将点变成点，求出矩阵。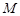

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省扬州市宝应县高三下学期期初测试数学试卷 题型：解答题

    （本题满分10分，选修4-2：矩阵与变换）

    已知二阶矩阵M属于特征值3的一个特征向量为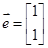，并且矩阵M对应的变换将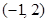点变成点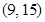，求出矩阵M.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省徐州市宿羊山高级中学高三学情调研数学试卷（1）（解析版） 题型：解答题

    [选做题]已知二阶矩阵M属于特征值3的一个特征向量为，并且矩阵M对应的变换将点（-1，2）变成点（9，15），求出矩阵M．

    查看答案和解析>>

    同步练习册答案