
分析 (1)由题意列关于p,q的方程组,求解方程组得p,q的值;
(2)把(1)中求得的p,q值代入Sn+1=pSn+q,取n=n-1得另一递推式,作差后可得数列{an}是等比数列,进一步得到通项公式;
(3)求出数列{an}的前n项和,代入λ≥$\frac{{S}_{n}}{n{a}_{n}}$,构造函数$f(n)=\frac{{{2^n}-1}}{n}$,利用作差法判断函数单调性,由单调性求得实数λ的取值范围.
解答 解:(1)由题意,得$\left\{\begin{array}{l}{S_2}=p{a_1}+q\\{S_3}=p{S_2}+q\end{array}\right.$,
即$\left\{\begin{array}{l}3=2p+q\\ 3+q-3p=3p+q\end{array}\right.$,解得$\left\{\begin{array}{l}p=\frac{1}{2}\\ q=2\end{array}\right.$;
(2)由(1)知,${S_{n+1}}=\frac{1}{2}{S_n}+2$,①
当n≥2时,${S_n}=\frac{1}{2}{S_{n-1}}+2$,②
①-②,得${a_{n+1}}=\frac{1}{2}{a_n}$(n≥2),
又 ${a_2}=\frac{1}{2}{a_1}$,
∴数列{an}是首项为2,公比为$\frac{1}{2}$的等比数列.
∴{an}的通项公式为${a_n}={({\frac{1}{2}})^{n-2}}$(n∈N*);
(3)由${a_n}={({\frac{1}{2}})^{n-2}}$,得${S_n}=4({1-\frac{1}{2^n}})$,
得$λ≥\frac{{1-\frac{1}{2^n}}}{{n\frac{1}{2^n}}}=\frac{{{2^n}-1}}{n}$,令$f(n)=\frac{{{2^n}-1}}{n}$,
∵$f({n+1})-f(n)=\frac{{({n-1}){2^n}+1}}{n(n+1)}>0$,∴f(n)为递增数列,
且$f(1)=1,\;f(2)=\frac{3}{2},\;f(3)=\frac{7}{3},\;f(4)=\frac{15}{4}$,
∴f(3)≤λ<f(4)即可,即 $λ∈[{\frac{7}{3},\;\frac{15}{4}})$.
点评 本题考查数列递推式,考查了等比数列的通项公式,考查数列的函数特性,是中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y=0或x+y-1=0 | B. | 2x-y=0或x+y-1=0 | ||
| C. | 2x+y=0或x-y+3=0 | D. | x+y-1=0或x-y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a5≥b5 | B. | a5≤b5 | C. | a5>b5 | D. | a5<b5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
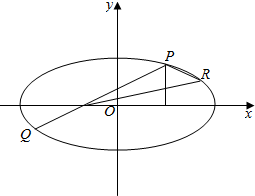 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点为F1、F2,过F2作垂直于x轴的直线交椭圆于P点(点P在x轴上方),连结PF1并延长交椭圆于另一点Q.设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$(2≤λ≤$\frac{7}{3}$).
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦点为F1、F2,过F2作垂直于x轴的直线交椭圆于P点(点P在x轴上方),连结PF1并延长交椭圆于另一点Q.设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$(2≤λ≤$\frac{7}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com